Приближенное решение матричной игры в смешанных стратегиях (модифицированный метод Брауна)
0. Общая характеристика условий применимости метода Брауна: приближенное решение с меньшими трудозатратами.
1. Описание метода Брауна
2. Алгоритм модифицированного метода Брауна:
2.1. Обозначения
2.2. Алгоритм
2.3. Пример
Модифицированный метод Брауна
О П Р Е Д Е Л Е Н И Я
Кп.1. Идея метода Брауна
Предназначен для поиска приближенных и оптимальных смешанных стратегий в матричной игре, где оперирующая (1-я) сторона стремится извлечь максимум выигрыша (максимум функции Fij), а 2-я сторона минимизировать этот выигрыш 1-ой стороны.
Первый игрок выбирает произвольно свою чистую стратегию i(1). Зная ее, 2-й игрок выбирает свою стратегию, стремясь минимизировать выигрыш 1-ого игрока. Здесь предполагается, что 2-й игрок лучше информирован о ходе игры, чем первый. Результат выбора – j(1). Первая итерация закончена.
На второй итерации считается что 1-й игрок знает ход противника j(1), первый игрок стремится максимизировать свой совокупный средний за два ходе выигрыш, выбором стратегии i(2). Второй игрок, предполагая, что 1-й игрок может с равной вероятностью использовать и стратегию i(1) и стратегию i(2). Т.о. 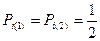 , выбирает свой ход i(1), минимизируя средний выигрыш 1-ого игрока за два года. Вторая итерация закончена.
, выбирает свой ход i(1), минимизируя средний выигрыш 1-ого игрока за два года. Вторая итерация закончена.
|
|
|
Далее первый игрок выбирает ход i(3), в предположении, что второй игрок применяет стратегии j(1) и j(2) с вероятностями 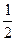 . Теперь второй игрок знает о выборе первым стратегий i(1), i(2), i(3) и выбирает свой ход j(3), полагая, что первый игрок применяет стратегии i(1), i(2), i(3) с вероятностями
. Теперь второй игрок знает о выборе первым стратегий i(1), i(2), i(3) и выбирает свой ход j(3), полагая, что первый игрок применяет стратегии i(1), i(2), i(3) с вероятностями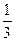 . Третья итерация закончена.
. Третья итерация закончена.
Доказано, что при этих условиях при числе итераций 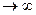 получаются оптимальные смешанные стратегии.
получаются оптимальные смешанные стратегии.
Кп/п2.1. Обозначения:
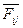 - элемент матрицы платежа (выигрыш 1-ого игрока при использовании 1-ой стороной стратегии i, а противником – стратегии j),
- элемент матрицы платежа (выигрыш 1-ого игрока при использовании 1-ой стороной стратегии i, а противником – стратегии j),
K – номер итерации в методе, (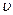 - тоже самое)
- тоже самое)
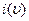 - номер стратегии, выбираемой 1-ой стороной на
- номер стратегии, выбираемой 1-ой стороной на 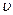 -ом шаге
-ом шаге
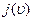 - номер стратегии, выбираемой 2-ой стороной на
- номер стратегии, выбираемой 2-ой стороной на 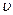 -ом шаге
-ом шаге
(тоже 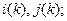
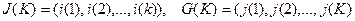 - последовательности чистых стратегий, применяемых 1-ой и 2-ой сторонами соответственно за К шагов,
- последовательности чистых стратегий, применяемых 1-ой и 2-ой сторонами соответственно за К шагов,
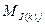 - возможный суммарный выигрыш 1-ой стороны за К шагов в ситуации, когда суммирование ведется с 1-ого по К-ый шаг при использовании 1-ой стороной последовательности чистых стратегий
- возможный суммарный выигрыш 1-ой стороны за К шагов в ситуации, когда суммирование ведется с 1-ого по К-ый шаг при использовании 1-ой стороной последовательности чистых стратегий 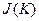 , а вторая сторона применяет всегда одну и ту же стратегию j,
, а вторая сторона применяет всегда одну и ту же стратегию j,
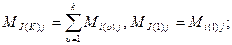 (1)
(1)
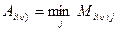 - гарантированный выигрыш 1-ой (2)
- гарантированный выигрыш 1-ой (2)
стороны на 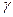 -ой итерации использования ею на
-ой итерации использования ею на 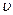 -ой итерации чистой стратегии
-ой итерации чистой стратегии 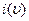 ;
;
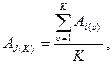 (3)
(3)
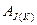 - средний за К шагов гарантированный выигрыш 1-ой стороны, при использовании ею чистых стратегий из
- средний за К шагов гарантированный выигрыш 1-ой стороны, при использовании ею чистых стратегий из 
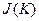 с равной вероятностью
с равной вероятностью 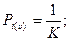

|
|
|
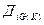 - возможный суммарный выигрыш 1-ой стороны за К шагов при условии, что суммирование выигрышей ведется с 1-ого по К-ый шаг, 2-ая сторона применяет последовательность чистых стратегий
- возможный суммарный выигрыш 1-ой стороны за К шагов при условии, что суммирование выигрышей ведется с 1-ого по К-ый шаг, 2-ая сторона применяет последовательность чистых стратегий 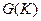 , а 1-ая сторона применяет одну и ту же чистую стратегию i,
, а 1-ая сторона применяет одну и ту же чистую стратегию i,
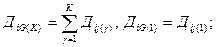 (4)
(4)
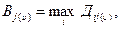 (5)
(5)
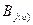 - максимальный возможный выигрыш 1-ой стороны на
- максимальный возможный выигрыш 1-ой стороны на 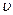 -ом шаге при использовании второй стороной стратегии
-ом шаге при использовании второй стороной стратегии 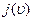 ,
,
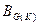 - максимальный средний за К шагов выигрыш 1-ой стороны при применении 2-ой стороной последовательности чистых стратегий G(K),
- максимальный средний за К шагов выигрыш 1-ой стороны при применении 2-ой стороной последовательности чистых стратегий G(K),
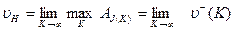 (6)
(6)
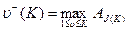 (7)
(7)
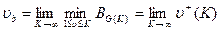 (8)
(8)
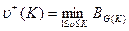 ;
; 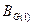 - очень большое число
- очень большое число
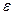 - заданная точность расчетов,
- заданная точность расчетов, 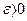 - достаточно малая положительная величина;
- достаточно малая положительная величина;
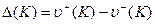 ,
,
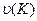 - цена игры за К шагов,
- цена игры за К шагов,
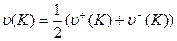 ,
,
Кп/п2.2. Алгоритм.
На 1-ой итерации выбираем произвольно i(1). При данном 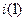 подсчитываем
подсчитываем 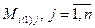 . Затем определяем
. Затем определяем 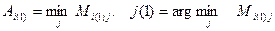 . При данном
. При данном 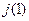 вычисляем величины
вычисляем величины 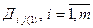 . Определяем
. Определяем 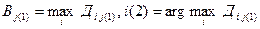 . Подсчитываем
. Подсчитываем 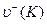 и
и 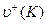 .
.
Конец первой итерации.
Эти данные заносим в таблицу.
| K | I(K) | MJ(K)1 | ….. | MJ(K)n | Ai(K) | J(K) | Д1 G(K) | …. | Дm G(K) | 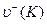
| 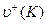
| 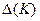
|
и т.д.
Расчеты заканчиваются, если 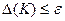 .
.
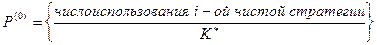
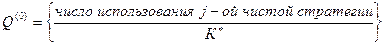
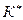 - номер итерации, где ……….
- номер итерации, где ……….
Кп.3. Пример
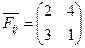
| K | i(k) | MJ(k)1 | MJ(k)2 | AJ(k) | j(k) | Д1 G(k) | Д2 G(k) | BG(k) | 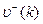
| 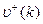
| 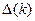
|
| 5/2=2,5 | 6/2=3 | 2,5 | 0,5 | ||||||||
| 6/3=2 | 8/3=2,66 | 2,5 | 2,66 | 0,16 | |||||||
| 10/4=2,5 | 10/4=2,5 | 2,5 | 2,5 | ||||||||
| не | делаем | т.к.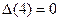
|
Оптимальные смешанные стратегии:
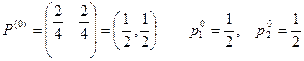

 2014-02-02
2014-02-02 615
615








