Решение матричной игры в смешанных стратегиях

Тема 5

Что можно предпринять, если цена не в состоянии скоординировать действия на рынке?

Лекция 10. Регулирование рынка

АНТОН. Теперь нам необходимо понять, что можно предпринять, если паучок уползает все дальше от точки равновесия.

ИГОРЬ. Совсем простой способ состоит в том, что государство закупает осенью часть урожая яблок, строит хранилища на рынке или рядом с ним и в любой момент может увеличить объем предложения, сбить цену, приостановить нарастание размаха колебаний цены вокруг ее равновесного уровня.

АНТОН. Можно, наверное, подсказывать продавцам завтрашнюю конъюнктуру, опираясь на обработку данных на компьютерах за прошлые периоды, или раз работать такие модели поведения потребителей в этом регионе, с помощью которых можно прогнозировать спрос.

ИГОРЬ. Да, возможностей подлечить рыночный организм много, вопрос только, чтобы он совсем не разболелся. Поэтому не стоит, как мне кажется, принимать слишком много лекарств.

АНТОН. Конечно. К тому же есть лекарства, которыми государство лечит весь государственный организм: деньги, бюджетное и правовое регулирование, а также многие другие. Если же только одна его часть не в порядке, дело можно поправить, воздействуя только на нее, например налогами или дотациями.

БАРБОС. Вот бы так подлечить рынок мяса и сосисок...

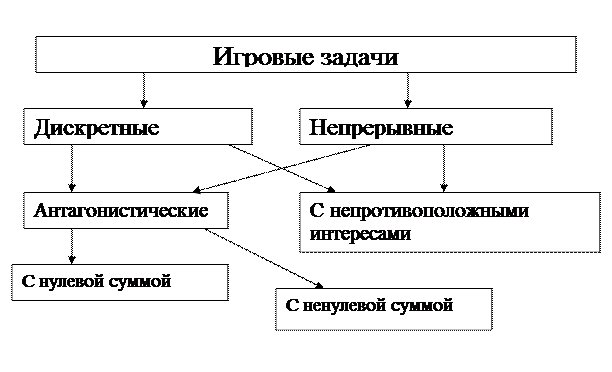
Определение 1(Игры задачи)

Игровые задачи – это задачи, в которых при управлении приходится учитывать наличие противодействующей стороны (сторон). Противодействие оперирующей стороне может быть стихийным и тогда игра называется игрой с природой. Противодействие может быть разумным и организованным. В этом случае игра называется игрой, с добавлением характеристики вида противодействия, числа противоборствующих сторон и характера множества возможных состояний.

Обозначения:

x – стратегия оперирующей стороны;

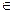x M, M 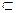E^m; E^m – пространство вещественных чисел размерности m

y – стратегия противника;

y 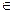N, N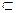Eⁿ; Eⁿ – пространство вещественных чисел размерности n.

F(x,y) – критериальная функция. Она же – функция выигрыша оперирующей стороны.

Определение 2

Если цели оперирующей стороны и ей противостоящей состоят в оптимизации одного и той же критериальной функции, причем оперирующая сторона стремится максимизировать, а вторая – минимизировать эту функцию, то игра называется антагонистической. Если выигрыш одного игрока равен проигрышу другого, то игра называется игрой с нулевой суммой. В такой игре проигрыш противной стороны есть F(x,y)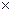(-1).

Определение 3

Ценой игры называется оптимальное значение F(x,y).

Определение 4

Нижней ценой игры называется минимальный гарантированный результат, на который может рассчитывать оперирующая сторона. Она равна

V_н = 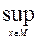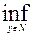F(x,y). (1)

Определение 5

Верхней ценой игры называется максимально возможный выигрыш оперирующей стороны при разумных действиях противника, выбирающего и реализующего свою стратегию, не зная о выборе оперирующей стороны. Она равна

V_в = 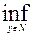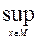F(x,y). (2)

Определение 6

Если sup и inf в выражениях (1) и (2) соответственно достижимы и

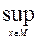
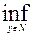F(x,y) =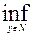 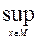F(x,y), т.е. V_н =V_в =V, то величина V называется ценой игры и говорят, что игра имеет седловую точку.

Теорема 1

Для того, чтобы V_н =V_в =V необходимо и достаточно существование пары точек х _с и у _с, для которых

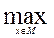F(x_c,y) = F(x_c,y_с) =F(x,y_c)

При этом F(x_c,y_с) = V_н =V_в =V, а х _с, у _с – наилучшие гарантирующие стратегии сторон, т.е. реализующие максимин и минимакс соответственно.

Теорема 2

Если М и N выпуклы, ограничены и замкнуты, а функция F(x,y) непрерывна и вогнута по х при каждом фиксированном у и выпукла по у при каждом фиксированном х, то F(x,y) имеет седловую точку.

Определение 7

Если функция F(x,y) представлена матрицей с m cтроками и n столбцами, определяющей выигрыш оперирующей стороны при выборе ею стратегии х_i, где i есть целые числа от 1 по m, а противником стратегии y_j, где j есть целые числа от 1 по n, то игра называется матричной игрой.

Далее матричное представление F(x,y) обозначается как 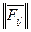и называется платежной матрицей.

Определение 8.

Пусть дана платежная матрица 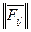с m строками и n столбцами. Смешанной стратегией оперирующей стороны называют вектор 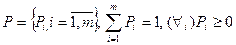. Смешанной стратегией противника называют вектор .

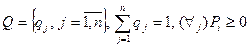Теорема3 (фон Неймана)

Любая матричная игра имеет седловую точку в смешанных стратегиях.

Теорема 4

Пусть 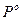и 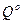оптимальные смешанные стратегии, V - цена игры. Тогда

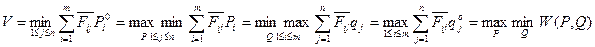(3)

Теорема 5

Решение матричной игры в смешанных стратегиях эквивалентно решению пары двойственных задач линейного программирования:

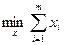
при ограничениях

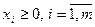
x_i=g_i (P_i,V),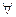 i.

Двойственная задача

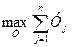
при

,

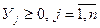Y_j = h_j (q_j,V), 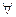j.

Доказательство.

Из теоремы 4 формула (3) следует:

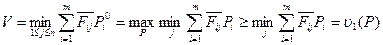
Здесь 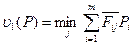(4)

Значит 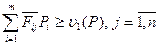(5)

Очевидно (из формулы (3)), что

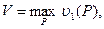т.е. (6)

решение матричной игры состоит в максимизации по 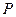величины .

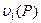Обозначим

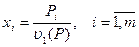(7)

Тогда деля на 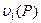обе части неравенства (5) (предполагая, что 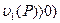, получим:

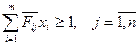(8)

Заметим, что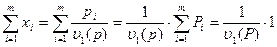

т.е.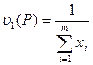

Тогда исходная задача эквивалентна

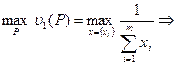
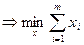(9)

при при

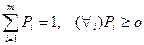
(8)

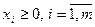(10)

Аналогично, из

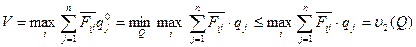
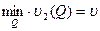(11)

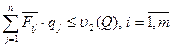(12)

Значит, полагая 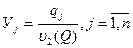и деля обе части неравенства (10) на 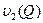получим, что

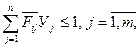(13)

Тогда задача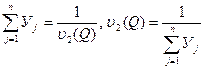

при

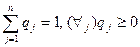
эквивалентна задаче

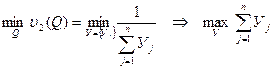(14)

при

(15)

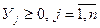
(16)

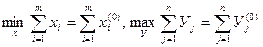
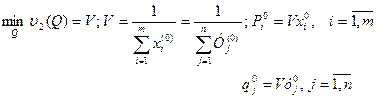
Что и требовалось доказать.

Пример

Найдем смешанную оптимальную стратегию противника: У⁽⁰⁾

Для этого решим задачу

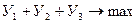
При

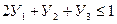
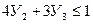
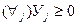
Превратим эту задачу в каноническую форму:

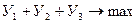
при

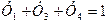
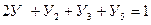
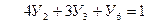
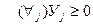
Составим таблицу Табл.1

								Cj 0
Б.П.	Сб	b	P1	P2	P3	P4	P5	P6
У4
У5
У6								Zj 1
								0
			-1	-1	-1

После преобразований имеем табл.2

Табл.2

Б.П.	Сб	b	P1	P2	P3	P4	P5	P6
У4		1/2		-1/2	5/2		-1/2
У1		1/2		1/2	1/2		½
У6								Zj 1
				1/2	1/2		½
				-1/2	-1/2		1/2	0

После преобразований имеем табл.3

Табл.3

								Cj 0
Б.П.	Сб	b	P1	P2	P3	P4	P5	P6
У4		5/8			23/8		-1/2	1/8
У1		3/8			1/8		½	-1/8
У2		1/4			3/4			¼
					7/8		½	Zj 1/8
					-1/8		1/2	1/8

После преобразований имеем табл.4

Cj

Табл.4

Б.П.	Сб	b	P1	P2	P3	P4	P5	P6
У3		5.23				8/23	4/23	1/23
У1		8/23				-1/23	1/23	-3/23
У2		2/23				-6/23	3/23	Zj 5/23
						1/23	11/23	3/23
						1/23	11/23	3/23

План оптимальный.

.

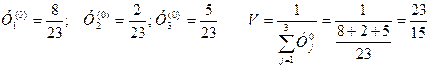
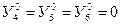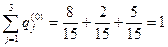
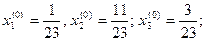Эти значения содержатся в табл.4:

Z₄ = x⁰₁, Z₅ = x⁰₂, Z₄ = x⁰₃.

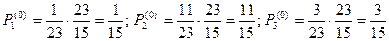
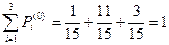
План лекции

1. Описание ситуации, в которой имеет смысл искать решение игры в смешанных стратегиях.

2. Понятие о смешанной стратегии. См.Определение 1, лист 2

Понятие о математическом ожидании платежа:

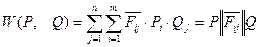
3. Теорема 1 фон Неймана и ее значение. См.Теорему 1 лист 2

4. Теорема 2 о цене игры: См.Теорему 2 лист 2

В предположении, что оперирующая сторона

Стремится максимизировать функцию ,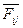

А противник – минимизировать

5. Эквивалентность решения матричной игры в смешанных стратегиях решению пары двойственных задач линейного программирования.

См.Доказательство на листе 3

6. О двойственности пары задач: (6)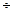(8) и (12)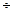(14)

А) коэф.лин.формы (=1) 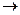в правые части другой

Б) число переем.одной = числу условий другой

В) обратные операторы оптимизации и знаки неравенств

Вывод. Решается лишь какая-то одна из них, а именно там, где число ограничений меньше либо равно числу переменных.

7. Пример. См.лист 4