Рассмотрим квадратную матрицу 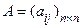 порядка n.
порядка n.
Опр. 1. Определителем или детерминантом n-го порядка матрицы А называется число 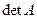
где сумма вычисляется по всем перестановкам вторых индексов. 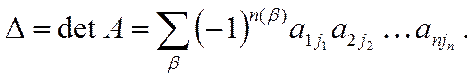
Обозначения определителя: 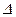 , det A, или в полной записи:
, det A, или в полной записи:
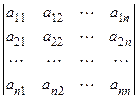 .
.
Используя определение определителя порядка n, получим формулы для вычисления определителей 2-го и 3-го порядка.
При n = 2 перестановок вторых индексов будет 2! = 2, одна четная – (12) и одна нечетная (21), следовательно:
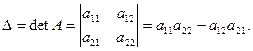 (1.4)
(1.4)
При n = 3. Следовательно:
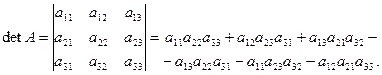 (1.5)
(1.5)
Опр. 2. Минором 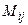 элемента
элемента 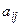 матрицы А называется определитель матрицы, полученной из матрицы А вычеркиванием i-й строки и j-гo столбца (т.е. строки и столбца, на пересечении которых находится этот элемент).
матрицы А называется определитель матрицы, полученной из матрицы А вычеркиванием i-й строки и j-гo столбца (т.е. строки и столбца, на пересечении которых находится этот элемент).
Например:
если 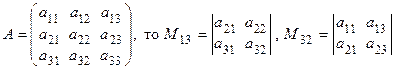 и т. д.
и т. д.
Опр. 3. (Алгебраическим дополнением 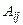 элемента
элемента 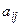 матрицы А называется число, равное
матрицы А называется число, равное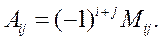
 2014-02-02
2014-02-02 415
415








