1.Вычислить определитель 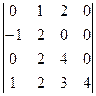
2. Обратная матрица.
Обратной матрицей A-1 к матрице A называется такая матрица, что:
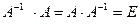 ,
Где E – единичная матрица.
Рассмотрим квадратную матрицу ,
Где E – единичная матрица.
Рассмотрим квадратную матрицу 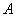 . Обратную матрицу . Обратную матрицу 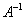 можно найти по следующей формуле: можно найти по следующей формуле:
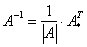 , где , где 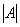 – определитель матрицы – определитель матрицы 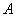 , , 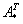 – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы 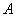 .
Понятие обратной матрицы существует только для квадратных матриц, матриц «два на два», «три на три» и т.д.
Пример:
Найти обратную матрицу для матрицы .
Понятие обратной матрицы существует только для квадратных матриц, матриц «два на два», «три на три» и т.д.
Пример:
Найти обратную матрицу для матрицы 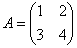 Решаем. Последовательность действий удобно разложить по пунктам.
1) Сначала находим определитель матрицы.
Решаем. Последовательность действий удобно разложить по пунктам.
1) Сначала находим определитель матрицы.
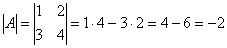 Важно! В том случае, если определитель матрицы равен НУЛЮ – обратной матрицы НЕ СУЩЕСТВУЕТ.
В рассматриваемом примере, как выяснилось,
Важно! В том случае, если определитель матрицы равен НУЛЮ – обратной матрицы НЕ СУЩЕСТВУЕТ.
В рассматриваемом примере, как выяснилось, 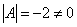 , а значит, всё в порядке.
2) Находим матрицу миноров , а значит, всё в порядке.
2) Находим матрицу миноров 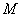 .
Матрица миноров имеет такие же размеры, как и матрица .
Матрица миноров имеет такие же размеры, как и матрица 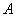 , то есть в данном случае , то есть в данном случае 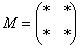 . Дело за малым, осталось найти четыре числа и поставить их вместо звездочек.
Возвращаемся к нашей матрице . Дело за малым, осталось найти четыре числа и поставить их вместо звездочек.
Возвращаемся к нашей матрице 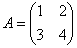 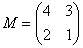 – матрица миноров соответствующих элементов матрицы – матрица миноров соответствующих элементов матрицы 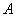 .
3) Находим матрицу алгебраических дополнений .
3) Находим матрицу алгебраических дополнений 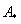 .
Это просто. В матрице миноров нужно ПОМЕНЯТЬ ЗНАКИ у двух чисел: .
Это просто. В матрице миноров нужно ПОМЕНЯТЬ ЗНАКИ у двух чисел: 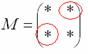
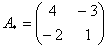 – матрица алгебраических дополнений соответствующих элементов матрицы – матрица алгебраических дополнений соответствующих элементов матрицы 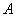 .
4) Находим транспонированную матрицу алгебраических дополнений .
4) Находим транспонированную матрицу алгебраических дополнений 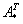 . .
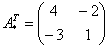 – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы 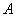 .
5) Ответ. Вспоминаем нашу формулу .
5) Ответ. Вспоминаем нашу формулу 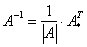 Таким образом, обратная матрица:
Таким образом, обратная матрица: 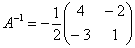 Как проверить решение?
Необходимо выполнить матричное умножение
Как проверить решение?
Необходимо выполнить матричное умножение 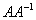 либо либо 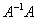 Получена так называемая единичная матрица (с единицами по главной диагонали и нулями в остальных местах).
Таким образом, обратная матрица найдена правильно.
Если провести действие
Получена так называемая единичная матрица (с единицами по главной диагонали и нулями в остальных местах).
Таким образом, обратная матрица найдена правильно.
Если провести действие 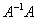 , то в результате тоже получится единичная матрица. Это один из немногих случаев, когда умножение матриц перестановочно. , то в результате тоже получится единичная матрица. Это один из немногих случаев, когда умножение матриц перестановочно.
|
1.7. Ранг матрицы
Рассмотрим прямоугольную матрицу 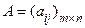 . Выберем в матрице А произвольно k строк с номерами i1, i2, …, ik и k столбцов с номерами j1, j2,..., jk, . Выберем в матрице А произвольно k строк с номерами i1, i2, …, ik и k столбцов с номерами j1, j2,..., jk, 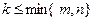 . Элементы, стоящие на пересечении выбранных строк и столбцов, образуют квадратную матрицу Аk порядка k.
Определитель матрицы Аk называется минором k-гo порядка (минором порядка k) и обозначается . Элементы, стоящие на пересечении выбранных строк и столбцов, образуют квадратную матрицу Аk порядка k.
Определитель матрицы Аk называется минором k-гo порядка (минором порядка k) и обозначается 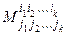 или, когда не важно, какие именно строки и столбцы выбраны, обозначается Mk, т.е. по определению Mk = det Аk. Например, если или, когда не важно, какие именно строки и столбцы выбраны, обозначается Mk, т.е. по определению Mk = det Аk. Например, если
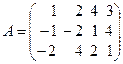 и выбраны строки c номерами i1 = 1, i2 = 3 и столбцы с номерами j1 = 2, j2 = 4, то
и выбраны строки c номерами i1 = 1, i2 = 3 и столбцы с номерами j1 = 2, j2 = 4, то
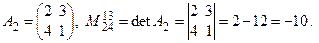 Число миноров второго порядка для этой матрицы равно 18.
Наивысший порядок миноров, не равных нулю, называется рангом матрицы и обозначается символами: rаng А или rA.
Из этого определения легко получить следующее правило для нахождения ранга матрицы: если найден минор порядка r не равный нулю и любой минор порядка r + 1 равен нулю, то ранг матрицы А равен r.
Пример 1.2. Найти ранг матрицы:
Число миноров второго порядка для этой матрицы равно 18.
Наивысший порядок миноров, не равных нулю, называется рангом матрицы и обозначается символами: rаng А или rA.
Из этого определения легко получить следующее правило для нахождения ранга матрицы: если найден минор порядка r не равный нулю и любой минор порядка r + 1 равен нулю, то ранг матрицы А равен r.
Пример 1.2. Найти ранг матрицы:
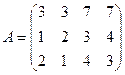 .
Решение. Здесь .
Решение. Здесь 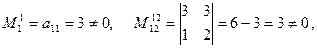
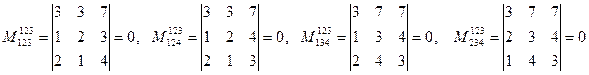 ,
следовательно rаng А = 2.
Вычисление ранга матрицы по определению приводит к очень громоздким и длительным вычислениям, поэтому чаще всего он вычисляется с помощью элементарных преобразований матрицы.
Элементарные преобразования матрицы:
1) перестановка (транспозиция) строк (столбцов) матрицы;
2) умножение всех элементов отроки (столбца) матрицы на действительное число ,
следовательно rаng А = 2.
Вычисление ранга матрицы по определению приводит к очень громоздким и длительным вычислениям, поэтому чаще всего он вычисляется с помощью элементарных преобразований матрицы.
Элементарные преобразования матрицы:
1) перестановка (транспозиция) строк (столбцов) матрицы;
2) умножение всех элементов отроки (столбца) матрицы на действительное число 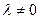 ;
3) прибавление к элементам строки (столбца) матрицы соответствующих элементов другой строки (столбца), умноженных на действительное число.
Утверждение 1.4. Элементарные преобразования не изменяют ранга матрицы. ;
3) прибавление к элементам строки (столбца) матрицы соответствующих элементов другой строки (столбца), умноженных на действительное число.
Утверждение 1.4. Элементарные преобразования не изменяют ранга матрицы.
|
Ввиду небольшого количества занятий и весьма нашей обширной программы курса следующая тема 4(Множества) предлагается для самостоятельного изучения.
Тема. 4. Множества.
Опр.1. Множеством называется совокупность некоторых элементов, объединенных каким-либо общим признаком. Элементами множества могут быть числа, фигуры, предметы, понятия и т.п.
Опр.2.1.2 Объекты, из которых состоит множество, называются его элементами (например, буква К – элемент множества бук в русского алфавита).
Обозначают множества заглавными буквами латинского алфавита или символически с помощью фигурных скобок, в которых указываются его элементы. Сами элементы некоторого множества будем обозначать малыми латинскими буквами, если они не имеют специальных обозначений:
А; {а, b, c}; {*,s,h,g}; N={1,2,3,4,5,6,7,8, …}.
Принадлежность предмета некоторому множеству обозначают с помощью символа Î (в противном случае используется символ Ï).
Запись аÎА означает, что а есть элемент множества А. Аналогично имеем: DÎ{,D,o}.
Запись 4Ï{1,2,3} означает, что 4 не принадлежит множеству {1,2,3}.
Основными способами задания множества являются:
1) перечисление всех его элементов: А={а1, а2, а3, …, аn};
2) описание (указание характеристического свойства его элементов). Этот способ требует указания такого признака, который имеется у всех элементов данного множества и не свойственен элементам, не входящим в данное множество. Например, характеристическим свойством натуральных чисел является возможность их использования при счете каких-либо предметов. Говоря о множестве четных чисел, мы указываем характеристическое свойство его элементов:
М={хÎN ½хM2}, т.е. каждое число, принадлежащее этому множеству, делится на два.
Опр.2.1.3 Множества, состоящие из одних и тех же элементов, называются равными (одинаковыми). Пишут А=В.
Опр.2.1.4 Множество, которое не содержит ни одного элемента, называется пустым и обозначается символом Æ.
 2014-02-02
2014-02-02 454
454








