Свойства определителей

Утверждение 1.3 (О разложении определителя по строке)

Определитель равен сумме попарных произведений элементов какой-либо строки на их алгебраические дополнения, т.е.

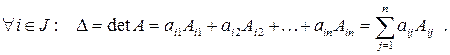(1.6)

1°. Определитель матрицы А равен определителю транспонированной матрицы 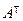, т. е.

det A = det.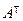

2°. Если хотя бы одна строка матрицы А состоит из нулей, то определитель этой матрицы равен нулю.

3°. °. Определитель матрицы, содержащей две одинаковые строки, равен нулю

4. При перестановке (транспозиции) любых двух строк в матрице, у определителя этой матрицы изменится знак.

5°. Если все элементы некоторой строки матрицы умножить на действительное число 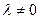, то определитель этой матрицы умножится на .

6°. Пусть матрицы А, В, С отличаются друг от друга только k-й строкой, причем элементы k-й строки матрицы С равны сумме соответствующих элементов k-х строк матриц А и В т.е.

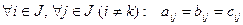
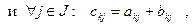
тогда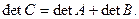

7°. Определитель матрицы не изменится, если к элементам какой-либо строки прибавить соответствующие элементы другой строки, умноженные на число .(8°. (Теорема аннулирования). Сумма произведений элементов, какой либо строки на алгебраические дополнения соответствующих элементов другой строки равна нулю, т.е.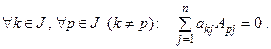) (1.7)

(8°. (Теорема аннулирования). Сумма произведений элементов, какой либо строки на алгебраические дополнения соответствующих элементов другой строки равна нулю, т.е.

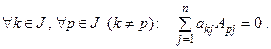) (1.7)

Опр. 5.Матрица называется невырожденной, если 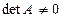, и вырожденной в противном случае.

Определитель выгоднее раскрывать по ТОЙ строке (столбцу), где:

1) нулей побольше;
2) числа поменьше.