Вариант решения 4.
Вариант решения 2.
Вариант решения 1.
Расчет с помощью матричных операций.
Использование матричной формы записи формул и проведения расчетов имеет несколько преимуществ и недостатков.
Преимущества заключаются в том, что запись формул приобретает очень компактный вид: вид формул, представленных в матричном виде, не зависит от количества факторов, включенных в модель, и является очень удобным при расчетах характеристик многофакторных моделей.
Недостатком использования в расчетах матричных формул является необходимость хорошего знания матричной алгебры.
Приведем перечень используемых матричных операций.
Транспонирование – Вставка функции, Категория: Ссылки и массивы, Функции: ТРАНСП.
Вычисление обратной матрицы - Вставка функции, Категория: Математические, Функции: МОБР.
Умножение матриц – Вставка функции, Категория: Математические, Функции: МУМНОЖ.
Выполнение матричных функций имеют следующие особенности:
- для результирующей матрицы нужно выделить необходимое количество ячеек;
- для распространения действий на массив:
Выделить 1-ю ячейку с расчетами и все ячейки, на которые будет распространено действие функции;
Нажать и отпустить клавишу «F2»;
Последовательно нажать, не отпуская, клавиши «Ctrl», «Shift», «Enter», отпустить все три клавиши, и на экране появится содержимое всей матрицы.
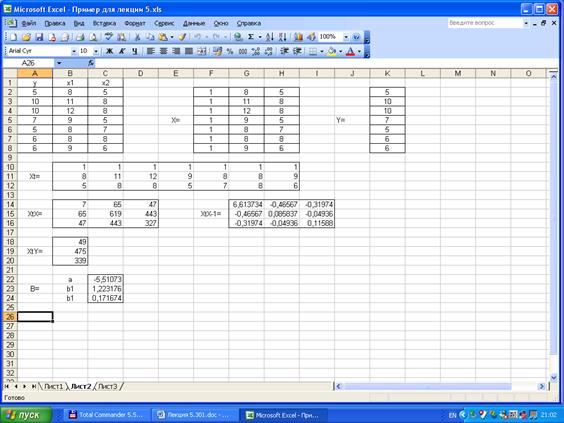
1) Составим 
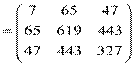 ,
,
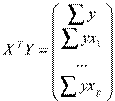
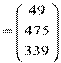 ,
, 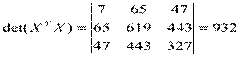 ,
,
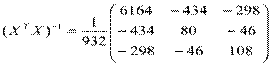 и
и
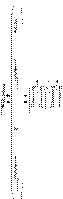
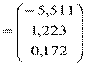 .
.
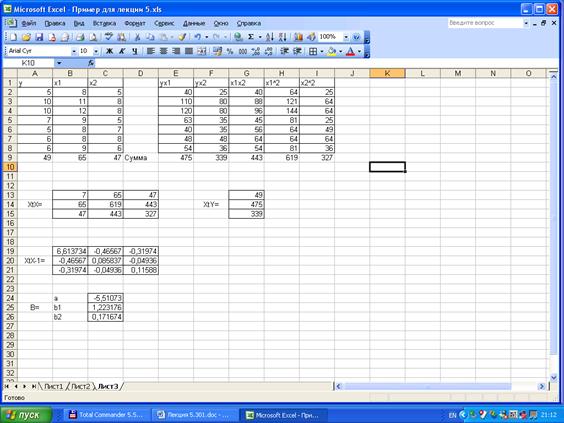
Таким образом, уравнение множественной регрессии примет вид:
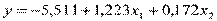 .
.
Вариант решения 3.
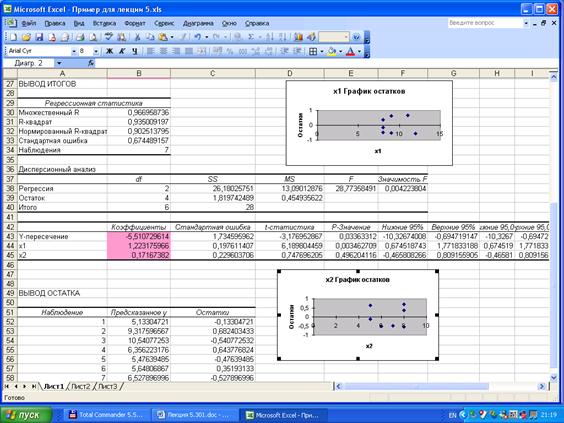
Получим уравнение регрессии в стандартизованном масштабе.
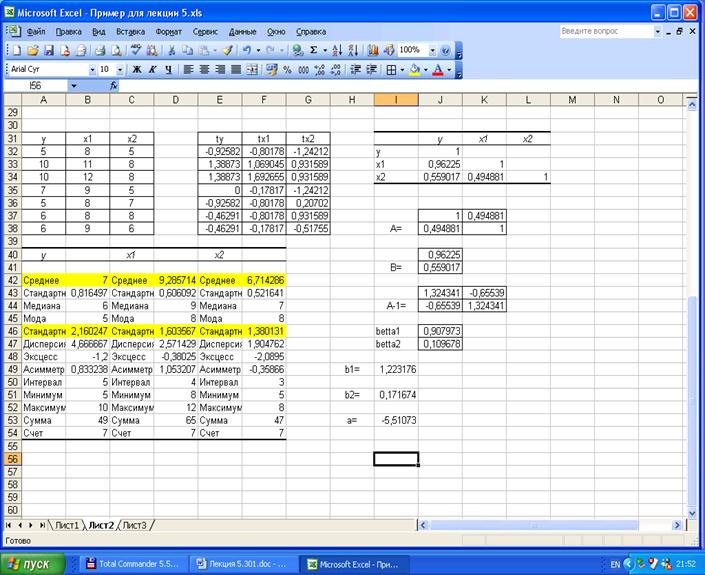
На практике часто бывает необходимо сравнение влияние на зависимую переменную различных объясняющих переменных, когда последние выражаются разными единицами измерения. В этом случае используют стандартизованные коэффициенты регрессии 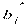 и средние показатели эластичности Эj:
и средние показатели эластичности Эj:
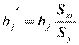 ,
, 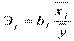 .
.
Стандартизованный коэффициент регрессии 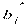 показывает, на сколько величин Sy изменится в среднем зависимая переменная Y при увеличении только j -й объясняющей переменной на Sxj, а средний показатель эластичности Эj – на сколько % (от средней) изменится в среднем Y при увеличении только Хj на1 %.
показывает, на сколько величин Sy изменится в среднем зависимая переменная Y при увеличении только j -й объясняющей переменной на Sxj, а средний показатель эластичности Эj – на сколько % (от средней) изменится в среднем Y при увеличении только Хj на1 %.
Пример.
Для данных предыдущего примера имеем:
1) 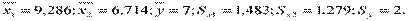
2) 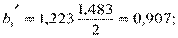
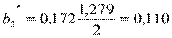 ;
;
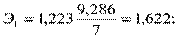
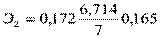 .
.
2. Ковариационная матрица оценок коэффициентов регрессии. Оценка дисперсии ошибок.
Преобразуем вектор оценок 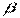 с учетом наличия случайной составляющей:
с учетом наличия случайной составляющей:
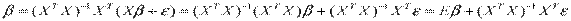 ,
,
Т.е. оценки параметров, найденные по выборке, будут содержать случайные ошибки.
Вариации оценок параметров будут определять точность уравнения множественной регрессии. Для их измерения в многомерном регрессионном анализе рассматривают ковариационную матрицу К, являющуюся матричным аналогом дисперсии одной переменной
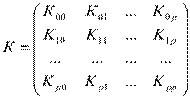 ,
, 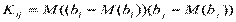 .
.
Ковариация характеризует как степень рассеяния значений двух переменных относительно их математических ожиданий, так и взаимосвязь этих переменных. Так как 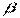 является несмещенной оценкой, то
является несмещенной оценкой, то
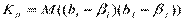 ,
, 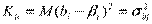 .
.
В матричном виде будем иметь
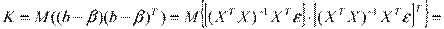
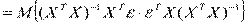
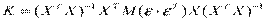 ,
,
так как эти элементы Х – детерминированные величины.
В матрице 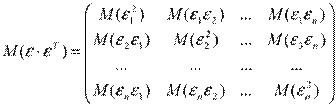 все элементы, не лежащие на главной диагонали, равны нулю в силу некоррелируемости
все элементы, не лежащие на главной диагонали, равны нулю в силу некоррелируемости 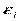 и
и 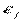 между собой, а все элементы, лежащие на главной диагонали равны одной и той же дисперсии
между собой, а все элементы, лежащие на главной диагонали равны одной и той же дисперсии 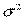 :
: 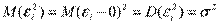 . Поэтому
. Поэтому 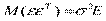 и, следовательно, ковариационная матрица
и, следовательно, ковариационная матрица
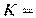
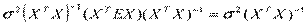 .
.
Так как 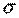 2 неизвестна, заменив её несмещённой оценкой – выборочной дисперсией,
2 неизвестна, заменив её несмещённой оценкой – выборочной дисперсией,
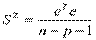 ,
,
где (n-p-1) – число степеней свободы, получим выборочную оценку ковариационной матрицы. Стандартные ошибки коэффициентов регрессии определяются:
1способ:  ,
, 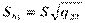 , …, где qii – диагональные элементы матрицы (ХТХ)-1.
, …, где qii – диагональные элементы матрицы (ХТХ)-1.
| 6,613734 | -0,46567 | -0,31974 | |||||||||
| XtX-1= | -0,46567 | 0,085837 | -0,04936 | ||||||||
| -0,31974 | -0,04936 | 0,11588 | |||||||||
| y^ | y-y^ | ||||||||||
| 1 | 5,133047 | -0,13305 | S^2= | 0,454936 | |||||||
| 2 | 9,317597 | 0,682403 | S= | 0,674489 | |||||||
| 3 | 10,54077 | -0,54077 | Sa= | 1,734596 | |||||||
| 4 | 6,356223 | 0,643777 | |||||||||
| 5 | 5,476395 | -0,47639 | Sb1= | 0,197611 | |||||||
| 6 | 5,648069 | 0,351931 | |||||||||
| 7 | 6,527897 | -0,5279 | Sb2= | 0,229604 | |||||||
| СУММКВ | 1,819742 | ||||||||||
2 способ: 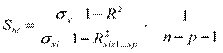 , где R2 – множественный коэффициент детерминации, R2xix1…xp – коэффициент детерминации для зависимости xi от остальных факторов.
, где R2 – множественный коэффициент детерминации, R2xix1…xp – коэффициент детерминации для зависимости xi от остальных факторов.
Предположим, что:
1. 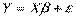 ;
;
2. Х – детерминированная матрица 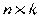 , имеющая максимальный ранг k;
, имеющая максимальный ранг k;
3. 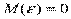 ;
; 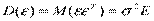 .
.
Тогда оценка МНК 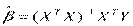 является наиболее эффективной (в смысле наименьшей дисперсии) оценкой в классе линейных несмещенных оценок.
является наиболее эффективной (в смысле наименьшей дисперсии) оценкой в классе линейных несмещенных оценок.
Доказательство:
Обозначим 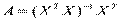 ,
, 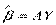 . Любую другую оценку
. Любую другую оценку 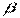 можно представить в виде
можно представить в виде 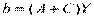 , где С – некоторая матрица.
, где С – некоторая матрица.
Докажем несмещенность оценок.
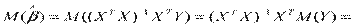
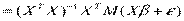
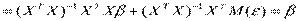 .
.
Так как оценка должна быть несмещенной, то
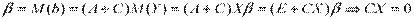 .
.
Используя СХ = 0, получим
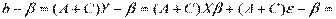
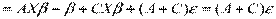
(так как AX = E и СХ = 0).
Вычислим ковариационную матрицу вектора b.
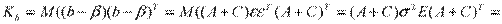
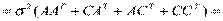
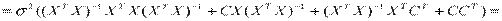
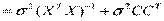 .
.
Таким образом, 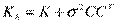 или
или 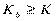 .
.
Теорема доказана.
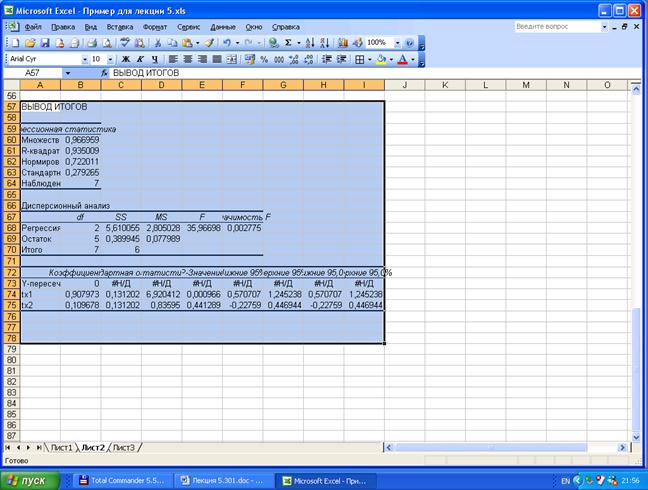
4. Коэффициент детерминации, скорректированный коэффициент детерминации.
Для оценки взаимосвязи между зависимой переменной и совокупностью объясняющих переменных используют множественный (совокупный) коэффициент (индекс) корреляции R или коэффициент детерминации R2. Как и раньше коэффициент детерминации R2 равен отношению 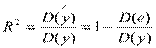 и характеризует долю вариации зависимой переменной, объясненную уравнением регрессии,
и характеризует долю вариации зависимой переменной, объясненную уравнением регрессии, 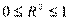 . Для расчета можно использовать более удобную формулу:
. Для расчета можно использовать более удобную формулу:
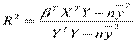 или
или 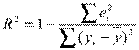 или
или 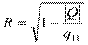 ,
,
где 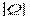 - определитель матрицы парных коэффициентов корреляции, q 11 – алгебраическое дополнение элемента r 11.
- определитель матрицы парных коэффициентов корреляции, q 11 – алгебраическое дополнение элемента r 11.
Множественный коэффициент детерминации можно рассматривать как меру качества уравнения регрессии, характеристику прогностической силы регрессионной модели. Чем ближе R2 к 1, тем лучше регрессия описывает зависимость между объясняющими и зависимой переменными.
Недостаток R2 состоит в том, что его значение не убывает с ростом числа объясняющих переменных. Это происходит потому, что:
1) оптимизация при определении оценок происходит по критерию, отличному от R2;
2) R2 возрастает при добавлении ещё одного регрессора и всегда можно добиться R2 = 1, что не будет иметь экономического смысла.
В этом смысле предпочтительней скорректированный коэффициент детерминации
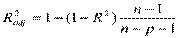 ,
,
который может уменьшаться при введении в регрессионную модель переменных, не оказывающих существенного влияния на зависимую переменную. Можно заметить, что 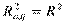 только при R2 = 1.
только при R2 = 1. 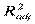 может принимать отрицательные значения (например, при R2 = 0). Для расчета можно использовать формулу:
может принимать отрицательные значения (например, при R2 = 0). Для расчета можно использовать формулу:
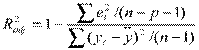 .
.
Пример. Вычислим коэффициент детерминации и скорректированный коэффициент детерминации  =
=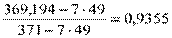 ; R = 0,967.
; R = 0,967.
 2014-02-02
2014-02-02 1296
1296








