классе всех линейных несмещенных оценок.
Доказательство:
1.
Докажем несмещенность оценок: 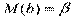 ,
, 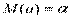 .
.
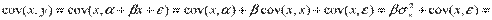
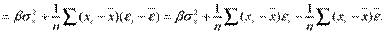
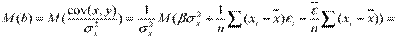
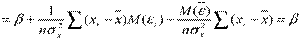 .
.
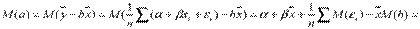
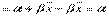 .
.
2. Определим дисперсии оценок.
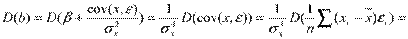
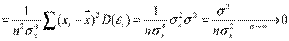 .
.
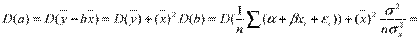
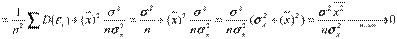 .
.
Следовательно, оценки состоятельны.
3. Оценки эффективны, то есть они имеют наименьшую дисперсию по сравнению с любыми другими оценками данных параметров.
2. Анализ точности определения оценок коэффициентов регрессии.
Так как выборочные данные являются случайными величинами, оценки 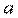 и
и 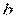 также являются случайными величинами. В случае выполнения условий Гаусса-Маркова, оценки будут несмещенными и состоятельными. При этом они будут тем надежнее, чем меньше их разброс вокруг их математических ожиданий или меньше их дисперсия. Надежность получаемых оценок тесно связана с D(
также являются случайными величинами. В случае выполнения условий Гаусса-Маркова, оценки будут несмещенными и состоятельными. При этом они будут тем надежнее, чем меньше их разброс вокруг их математических ожиданий или меньше их дисперсия. Надежность получаемых оценок тесно связана с D(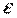 ). Как уже известно
). Как уже известно 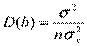 ,
, 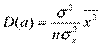 . Из соотношений можно сделать следующие очевидные выводы:
. Из соотношений можно сделать следующие очевидные выводы:
1) дисперсии 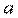 и
и 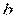 прямо пропорциональны D(
прямо пропорциональны D(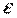 ) =
) =  2;
2;
2) чем больше число наблюдений, тем меньше дисперсия;
3) чем больше 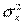 (разброс х), тем меньше дисперсии оценок.
(разброс х), тем меньше дисперсии оценок.
Так как случайные составляющие по выборке определены быть не могут, при анализе надёжности оценок коэффициентов регрессии они заменяются наблюдаемыми отклонениями 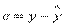 , а дисперсии случайных отклонений D(
, а дисперсии случайных отклонений D(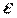 ) =
) =  2 заменяются несмещенной оценкой
2 заменяются несмещенной оценкой 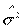 =
= 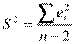 (здесь (n-2) – число степеней свободы). S – называют стандартной ошибкой регрессии. Тогда оценки дисперсий оценок
(здесь (n-2) – число степеней свободы). S – называют стандартной ошибкой регрессии. Тогда оценки дисперсий оценок
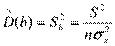 и
и 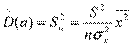 ,
,
S a и Sb – стандартные ошибки коэффициентов регрессии.
Пример. Получим оценки S2, S a, Sb для условий примера из лекции 2.
| № предприятия | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Выпуск продукции, х | 1 | 2 | 4 | 3 | 5 | 3 | 4 |
| Затраты на производство, у | 30 | 70 | 150 | 100 | 170 | 100 | 150 |
Решение
Ранее было получено уравнение регрессии
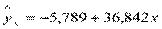 , с использованием которого можно было рассчитать модельные значения
, с использованием которого можно было рассчитать модельные значения 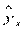 . Чтобы получить стандартные ошибки, необходимо:
. Чтобы получить стандартные ошибки, необходимо:
1) 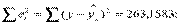 n = 7;
n = 7;
S2 = 263,1583/5 = 52,632; S = 7,255;
2) 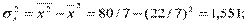
3) Sb2 = 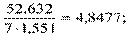 Sb = 2,202;
Sb = 2,202;
4) S a 2 = 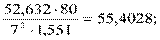 S a = 7,443.
S a = 7,443.
Стандартные ошибки регрессии и её коэффициентов можно получить при использовании ППП Excel (см. Вывод итогов).
Если выполняется условие нормальности распределения случайного члена: 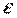 ~ N(0;
~ N(0; 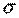 ), то МНК оценки коэффициентов регрессии тоже нормальны с соответствующими параметрами, так как они являются линейными функциями от Уt:
), то МНК оценки коэффициентов регрессии тоже нормальны с соответствующими параметрами, так как они являются линейными функциями от Уt:
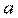 ~ N(
~ N(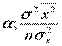 ) и
) и 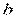 ~ N(
~ N(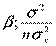 ).
).
Если условие нормальности ошибок не выполняется, то при некоторых условиях регулярности и росте n можно считать это распределение асимптотически нормальным.
Во время статистических исследований всегда проверяют гипотезы:
Н0: а = а 0 или «о значимости» Н0: а = 0
Н0: b = b0 Н0: b = 0.
Альтернативная гипотеза (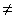 ) предусматривает построение двусторонней критической области. В качестве критерия проверки используют случайные величины, называемые
) предусматривает построение двусторонней критической области. В качестве критерия проверки используют случайные величины, называемые
| ВЫВОД ИТОГОВ | ||||||
| Регрессионная статистика | ||||||
| Множественный R | 0,991189256 | |||||
| R-квадрат | 0,98245614 | |||||
| Нормированный R-квадрат | 0,978947368 | |||||
| Стандартная ошибка | 7,254762501 | |||||
| Наблюдения | 7 | |||||
| Дисперсионный анализ | ||||||
| df | SS | MS | F | Значимость F | ||
| Регрессия | 1 | 14736,84211 | 14736,84211 | 280 | 1,39294E-05 | |
| Остаток | 5 | 263,1578947 | 52,63157895 | |||
| Итого | 6 | 15000 | ||||
| Коэффициенты | Стандартная ошибка | t-статистика | P-Значение | Нижние 95% | Верхние 95% | |
| Y-пересечение | -5,789473684 | 7,443229276 | -0,777817459 | 0,47185877 | -24,92290365 | 13,34395628 |
| x | 36,84210526 | 2,201736912 | 16,73320053 | 1,39294E-05 | 31,18236035 | 42,50185017 |
t-статистиками: tb = 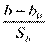 или ta =
или ta = 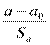 ; которые имеют распределение Стьюдента с (n-2) степенями свободы. Проверка состоит в следующем:
; которые имеют распределение Стьюдента с (n-2) степенями свободы. Проверка состоит в следующем:
- если 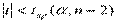 , то нет оснований отвергать Н0;
, то нет оснований отвергать Н0;
- если 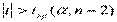 , то Н0 отвергают.
, то Н0 отвергают.
При оценке значимости коэффициентов линейной регрессии на начальном этапе можно использовать «грубое» правило:
1) если стандартная ошибка коэффициента больше его по модулю (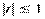 ), то коэффициент не значим (надежность меньше 0,7);
), то коэффициент не значим (надежность меньше 0,7);
2) если 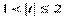 , то оценка может рассматриваться как относительно значимая, 0,7 <
, то оценка может рассматриваться как относительно значимая, 0,7 <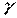 <0,95;
<0,95;
3) 2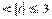 , то оценка значима, 0,95 <
, то оценка значима, 0,95 <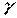 <0,99;
<0,99;
4) 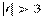 , это почти гарантия наличия линейной связи.
, это почти гарантия наличия линейной связи.
В каждом конкретном случае имеет значение число наблюдений. Чем их больше, тем надежнее при прочих равных условиях выводы о значимости коэффициентов. При n>10 «грубое» правило практически всегда работает.
Соответствующие доверительные интервалы для оценок коэффициентов регрессии с надёжностью 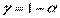 имеют вид: (
имеют вид: (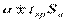 ) и (
) и (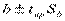 ).
).
Пример. Проверим гипотезу Н0: b = 37 при  и 0,05 для нашего примера.
и 0,05 для нашего примера.
1) 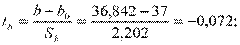
2) tкр.дв(0,01;5) = 4,03; tкр.дв(0,05;5) = 2,57;
3) Так как 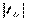 = 0,072 < tкр.дв(0,05;5) = 2,57, то нет оснований отвергать Н0.
= 0,072 < tкр.дв(0,05;5) = 2,57, то нет оснований отвергать Н0.
Если Н0 отвергается при  , то она будет отвергнута и при
, то она будет отвергнута и при 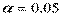 . Если Н0 не отвергается при
. Если Н0 не отвергается при 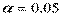 , то она не будет отклоняться и при
, то она не будет отклоняться и при 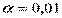 автоматически. Стандартные ППП содержат проверку «значимости» полученных оценок. При этом если Н0: b = 0 не отклоняется, то коэффициент b статистически не значим, то есть нет зависимости между Х и У.
автоматически. Стандартные ППП содержат проверку «значимости» полученных оценок. При этом если Н0: b = 0 не отклоняется, то коэффициент b статистически не значим, то есть нет зависимости между Х и У.
3. Качество уравнения регрессии. Коэффициент детерминации.
Цель регрессионного анализа состоит в объяснении поведения зависимой переменной. Пусть для этого по выборочным данным построено уравнение регрессии. Тогда значение у в каждом наблюдении можно разложить на две составляющие 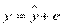 , где е – остаток, т.е. та часть, которую невозможно объяснить. Разброс значений зависимой переменной характеризуется выборочной дисперсией
, где е – остаток, т.е. та часть, которую невозможно объяснить. Разброс значений зависимой переменной характеризуется выборочной дисперсией
D(y) = D (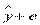 ) = D (
) = D (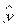 ) + D (e) + 2cov (
) + D (e) + 2cov (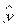 , e).
, e).
Cov (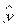 , e) = cov (
, e) = cov (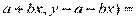
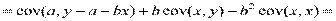
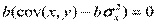
D(y) = D(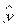 ) + D(e)
) + D(e)
общая дисперсия факторная дисперсия, остаточная дисперсия,
объясненная уравнением необъясненная
Коэффициентом детерминации R2 называют отношение 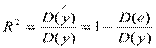 ,
,
характеризующее долю вариации зависимой переменной, объясненную уравнением регрессии, 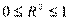 .
.
Если R2 = 1, то D(y) = D(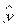 ), D(e) = 0, т.е. все точки наблюдений лежат на регрессионной прямой.
), D(e) = 0, т.е. все точки наблюдений лежат на регрессионной прямой.
Если R2 = 0, то регрессия не дает ничего, линия регрессии параллельна оси Ох.
Чем ближе R2 к 1, тем более точно 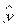 аппроксимирует у.
аппроксимирует у.
Вычисление R2 корректно, если 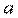 включено в уравнение. Полезны следующие соотношения:
включено в уравнение. Полезны следующие соотношения:
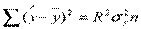 ;
; 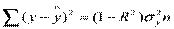 ;
; 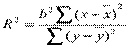 .
.
Для определения статистической значимости R2 проверяется гипотеза
Н0: R2 = 0 с помощью статистики F = 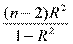 .
.
Если F < Fкр(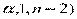 , то Н0 нет оснований отвергать или R2 статистически не значим, в противном случае – значим. В случае парной регрессии R2 = r 2. Коэффициент корреляции r выступает показателем тесноты линейной зависимости, тесная нелинейная связь возможна и при r, близких к нулю.
, то Н0 нет оснований отвергать или R2 статистически не значим, в противном случае – значим. В случае парной регрессии R2 = r 2. Коэффициент корреляции r выступает показателем тесноты линейной зависимости, тесная нелинейная связь возможна и при r, близких к нулю.
Для нашего примера:
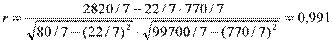 , R2 = 0,982.
, R2 = 0,982.
Следовательно, уравнение регрессии описывает 98,2% дисперсии признака у. Это означает очень тесную зависимость.
Можно показать, что в парном регрессионном анализе эквивалентны t-критерий для Н0: b = 0, t-критерий для Н0: r = 0 и F-критерий для Н0: R2 = 0. Таким образом, проверка значимости коэффициента b равносильна проверке значимости уравнения регрессии
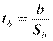 ,
, 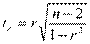 , F =
, F = 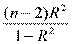 и tb = tr =
и tb = tr = 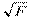 .
.
4. Интервалы прогноза по линейному уравнению регрессии.
Одной из центральных задач эконометрики является прогнозирование значений зависимой переменной при определенных значениях объясняющих переменных. Различают точечное и интервальное прогнозирование. При этом возможно предсказать условное математическое ожидание зависимой переменной (т.е. ср. значение), либо прогнозировать некоторое конкретное значение (т.е. индивидуальное).
Пусть имеется уравнение регрессии 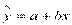 . Точечной оценкой М(У│Х=хр) =
. Точечной оценкой М(У│Х=хр) = 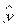 р =
р = 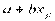 . Так как
. Так как 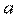 и
и 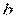 имеют нормальное распределение (в силу нормальности
имеют нормальное распределение (в силу нормальности 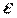 ), то
), то 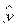 р является случайной величиной с нормальным распределением.
р является случайной величиной с нормальным распределением.
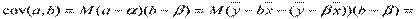
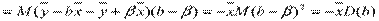 ,
,
М(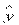 р) = М(
р) = М(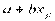 ) =
) = 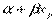
D(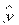 р) = D(
р) = D(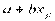 ) + D(
) + D(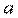 ) + xp2D(
) + xp2D(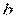 ) + 2cov(
) + 2cov(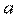 ,
,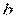 )xp =
)xp = 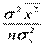 +
+
+ xp2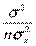 -2xp
-2xp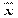
 =
=  (
(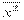 + xp2 - 2 xp
+ xp2 - 2 xp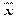 )│
)│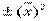 =
=
= 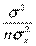 (
(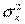 +
+ 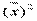 - 2 xp
- 2 xp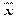 + xp2) =
+ xp2) = 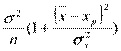 .
.
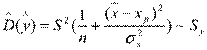 - стандартная ошибка положения линии регрессии. Так как она минимальна при хр =
- стандартная ошибка положения линии регрессии. Так как она минимальна при хр = 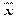 , то наилучший прогноз находится в центре области наблюдений и ухудшается по мере удаления от центра.
, то наилучший прогноз находится в центре области наблюдений и ухудшается по мере удаления от центра.
Случайная величина 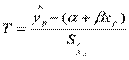 имеет распределение Стьюдента с (n-2) степенями свободы. Поэтому, задавая
имеет распределение Стьюдента с (n-2) степенями свободы. Поэтому, задавая 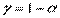 = Р(
= Р(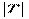 <tкр(
<tкр(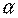 , n-2)), можно построить доверительный интервал для М(У│Х = хр), то есть положения линии регрессии (рис. 1.): (
, n-2)), можно построить доверительный интервал для М(У│Х = хр), то есть положения линии регрессии (рис. 1.): (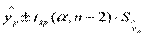 )
)
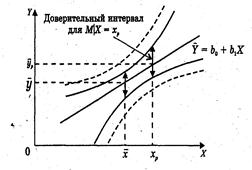
Рис. 1. Доверительные интервалы положения линии регрессии – сплошная линия и индивидуального значения – пунктирная линия.
Фактические значения у варьируются около среднего значения 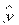 р. Индивидуальные значения у могут отклоняться от
р. Индивидуальные значения у могут отклоняться от 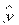 р на величину случайной ошибки
р на величину случайной ошибки 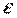 . Пусть yi - некоторое возможное значение у при хр. Если рассматривать yi как случайную величину У, а
. Пусть yi - некоторое возможное значение у при хр. Если рассматривать yi как случайную величину У, а 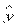 р – как случайную величину Ур, то можно отметить, что:
р – как случайную величину Ур, то можно отметить, что:
Y ~ N(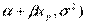 , Yp ~ N(
, Yp ~ N(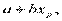
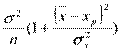 ).
).
Y и Yp независимы и, следовательно, U = Y - Yp ~ N с параметрами
M(U) = 0; D(U) = 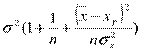 .
.
Значит 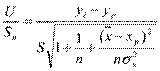 случайная величина, имеющая распределение Стьюдента с (n-2) степенями свободы. Аналогично строится доверительный интервал индивидуального значения.
случайная величина, имеющая распределение Стьюдента с (n-2) степенями свободы. Аналогично строится доверительный интервал индивидуального значения.
Пример. Стандартная ошибкасреднего расчетного значения
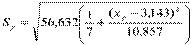 .
.
При 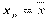 ,
, 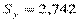 . При
. При 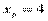 ,
, 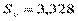 . Следовательно,
. Следовательно, 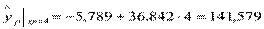 и, т.к.
и, т.к. 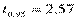 , то
, то 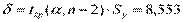 и
и
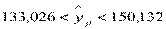 .
.
Стандартная ошибка индивидуального расчетного значения
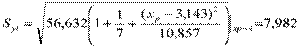 ,
,
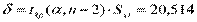 и
и 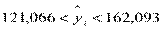 .
.
Фактические значения результативного признака отличаются от теоретических, рассчитанных по уравнению регрессии. Для сравнения используются величины отклонений, выраженные в процентах к фактическим значениям. Поскольку 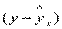 может быть как положительной, так и отрицательной величиной, ошибки аппроксимации для каждого наблюдения принято определять в процентах по модулю.
может быть как положительной, так и отрицательной величиной, ошибки аппроксимации для каждого наблюдения принято определять в процентах по модулю.
Для того чтобы иметь общее суждение о качестве модели из относительных отклонений по каждому наблюдению, находят среднюю ошибку аппроксимации как среднюю арифметическую простую.
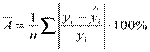 .
.
Допустимый предел 8 – 10 %, при котором подбор модели к исходным данным считается хорошим.
Возможно и другое определение средней ошибки аппроксимации:
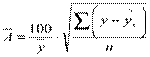 .
.
Рассчитаем среднюю ошибку аппроксимации для нашего примера.
| № | y | 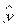 | 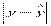 | 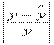 |
| 1 | 30 | 31,053 | 1,053 | 0,035 |
| 2 | 70 | 67,895 | 2,105 | 0,030 |
| 3 | 150 | 141,579 | 8,421 | 0,056 |
| 4 | 100 | 104,737 | 4,737 | 0,047 |
| 5 | 170 | 178,421 | 8,421 | 0,049 |
| 6 | 100 | 104,737 | 4,737 | 0,047 |
| 7 | 150 | 141,579 | 8,421 | 0,056 |
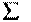 | 0,322 |
Окончательно получим: 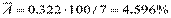 , что говорит о хорошем качестве уравнения.
, что говорит о хорошем качестве уравнения.
Выборочный коэффициент вариации определяется отношением выборочного среднего квадратического отклонения к выборочной средней, выраженным в процентах:
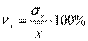 и
и 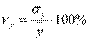 .
.
Коэффициент вариации – безразмерная величина, удобная для сравнения величин рассеивания двух и более выборок, имеющих разные размерности. Совокупность данных считается однородной и пригодной для использования МНК и вероятностных методов оценок статистических гипотез, если значение коэффициента вариации не превосходит 35 %.
Для нашего примера:
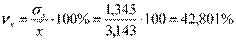 ,
,
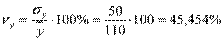 .
.
Пример. Фирма провела рекламную компанию. Через 10 недель фирма решила проанализировать эффективность этого вида рекламы, сопоставив недельные объемы продаж (у, тыс. руб.) с расходами на рекламу (х, тыс. руб.).
Полагая, что между переменными х и у имеет место линейная зависимость, определить выборочное уравнение регрессии.
| х | 5 | 8 | 6 | 5 | 3 | 9 | 12 | 4 | 3 | 10 |
| у | 72 | 76 | 78 | 70 | 68 | 80 | 82 | 65 | 62 | 90 |
Решение см. в Excel.
 2014-02-02
2014-02-02 1551
1551








