2014-02-02
2604
В случае парной регрессии естественной мерой зависимости (линейной) является выборочный коэффициент корреляции между переменными. Использование многомерной регрессии позволяет обобщить это понятие на случай, когда имеется несколько независимых переменных. Корректировка здесь необходима по следующим соображениям: высокое значение коэффициента корреляции между исследуемой зависимой и какой-либо независимой переменной может означать высокую степень зависимости, но может быть обусловлено и другой причиной. Имеется третья переменная, которая оказывает сильное влияние на две первые, что и является причиной высокой корреляции.
Поэтому возникает естественная задача найти «чистую» корреляцию между двумя переменными, исключив (линейное) влияние других факторов. Это можно сделать с помощью коэффициента частной корреляции.
Показатели частной корреляции представляют собой отношение сокращения остаточной дисперсии за счет дополнительного включения в анализ нового фактора к остаточной дисперсии, имевшей место до введения его в модель.
Пусть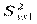 
, 
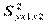- соответствующие остаточные дисперсии регрессий Y на X1 и Y на X1, X2. Влияние фактора X2 на результат можно определить коэффициентом частной корреляции
, 
.
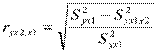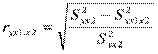Можно получить другую формулу коэффициента частной корреляции:
, 
Или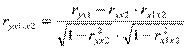 
, 
.
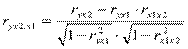Рассмотренные показатели частной корреляции называют коэффициентами частной корреляции 1-го порядка, так как они фиксируют тесноту связи двух переменных при закреплении (элиминировании) влияния одного фактора. Порядок частного коэффициента корреляции определяется количеством факторов, влияние которых исключается. Коэффициенты парной корреляции называют коэффициентами нулевого порядка. Если рассматривается регрессия с числом факторов р, то возможны частные коэффициенты корреляции 1-го, 2-го, …, (р-1)-го порядков, т.е. влияние, например, х1 можно оценить при разных условиях независимости действия других факторов: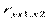 
, 
, 
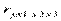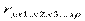. Сопоставление коэффициентов частной корреляции разного порядка по мере увеличения числа включаемых факторов показывает процесс «очищения» зависимости результативного признака с исследуемым фактором.
Выборочным частным коэффициентом корреляции между переменными xi и xj при фиксированных значениях остальных (р-2) переменных называют выражение
,
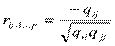где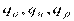 
- алгебраические дополнения элементов 
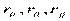матрицы выборочных коэффициентов корреляции. Коэффициенты частной корреляции более высоких порядков можно определить через коэффициенты частной корреляции более низких порядков по рекуррентной формуле:
.
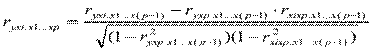В частности, при трех факторах возможно вычисление трех коэффициентов частной корреляции 2-го порядка: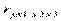 
, 
, 
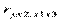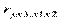, например,
.
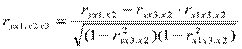Например. Составим матрицу Q парных коэффициентов корреляции, частные коэффициенты корреляции.
; 
; 
; 
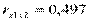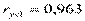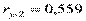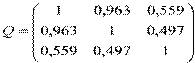; det(Q)=0,04823; q 11 = 1-0,4972 = 0,75299;
R =.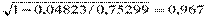
.
; 
; 
.
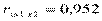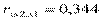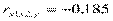Сравнивая частные коэффициенты корреляции с соответствующими парными коэффициентами, видим, что за счет «очищения» связи наибольшему изменению подвергся коэффициент корреляции между х1 и х2: был 0,497 – стал -0,185. Это пример ложной корреляции, так как х1 – мощность пласта не может зависеть от х2 – уровня механизации. А коэффициенты корреляции между у и х1, у и х2 после «очищения» несколько снизились от 0,963 до 0,952 и от 0,599 до 0,344, что по-видимому, соответствует действительности.
Зная частные коэффициенты корреляции, можно определить совокупный коэффициент корреляции по формуле:
.
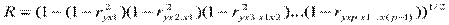6. Проверка статистических гипотез, доверительные интервалы.
Проверка значимости коэффициентов регрессии.
Как и в случае парной регрессии можно показать, что вектор оценок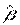 
имеет нормальное распределение со средним 
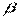и матрицей ковариаций 
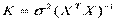, т е.
.
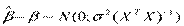Таким образом, случайные величины
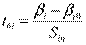и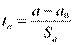 
имеют распределение Стьюдента с (n-р-1) степенями свободы. В общем случае проверяются гипотезы: Н0: а = а 0 или о значимости Н0: а = 0
Н0: b = b0 Н0: b = 0
Проверка состоит в следующем:
- если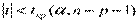 
, то нет оснований отвергать Н0 (р - число факторов);
- если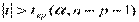 
, то Н0 отвергают.
Соответствующие доверительные интервалы для оценок коэффициентов регресси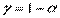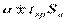и (
): (
) и (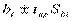
).
Пример.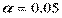 
, k = n – p – 1 = 7-2-1 = 4, tkp(0,05;4) = 2,78.
1) H0: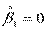 
, 
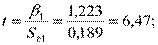
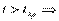Н0 отвергается и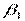 
значим при 5 - % -ом уровне значимости.
Доверительный интервал: (0,698; 1,748).
2.
H0: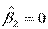 
, 
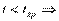Н0 принимается и
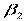не значим.
Доверительные интервалы.
Наряду с интервальным оцениванием коэффициентов регрессии весьма важным для оценки точности определения зависимой переменной является построение доверительного интервала для функции регрессии или условного математического ожидания зависимой переменной Мх(y). Обобщая соответствующие выражения на случай множественной регрессии, можно получить доверительный интервал:
,
, 
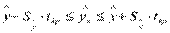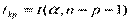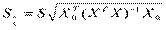- стандартная ошибка, 
.
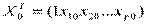Доверительный интервал для индивидуальных значений зависимой переменной yi примет вид: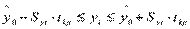 
, 
.
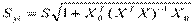Доверительный интервал для параметра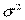 
во множественной регрессии строится аналогично парной модели: 
.
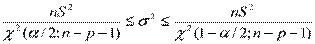Пример. Известно: S2 = 0,4175; S = 0,64614;
; 
.
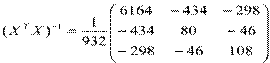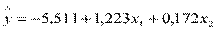По данным примера оценить сменную добычу угля на одного рабочего для шахт с мощностью пласта 10 м и уровнем механизации 6,5 %. Найти 95 % -й доверительный интервал для индивидуального и среднего значений и интервальную оценку дисперсии при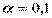 
.
1) 
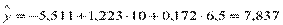(т).
2) 
, 
,
=
.
, 
.
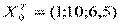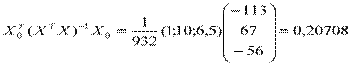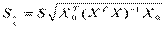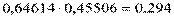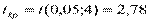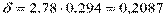3) 
; 
.
.
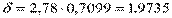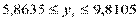4) 
; 
; 
; 
;
;
;
; 
.
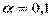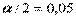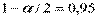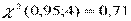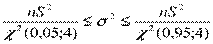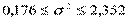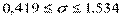Оценка надежности результатов множественной регрессии и корреляции.
Для определения статистической значимости R2 проверяется гипотеза
Н0: R2 = 0 с помощью статистики F =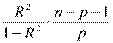 
.
Если F < Fкр(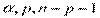
), то Н0 нет оснований отвергать или R2 статистически не значим, не значимо и уравнение в целом. В противном случае – уравнение и R2 значимы.
Пример.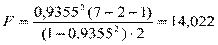 
. Fkp (0,05;2;4) = 6,94.
Т.к. F > Fkp, то уравнение значимо.
Оценивается не только значимость уравнения в целом, но и значимость фактора, дополнительно включенного в модель. Мерой оценки включения фактора в модель служит частный F- критерий, Fxi.
Если оценивается значимость влияния фактора хр после включения в модель факторов х1, х2,…,хр-1, то формула частного F- критерия примет вид:
.
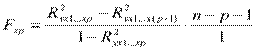В общем виде для xi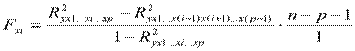 
.
С помощью частного F- критерия можно проверить значимость всех коэффициентов регрессии в предположении, что каждый соответствующий фактор вводится в уравнение последним. Зная Fxi можно определить t-критерий: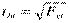 
. Взаимосвязь частного коэффициента корреляции, частного F-критерия и t-критерия для коэффициентов чистой регрессии можно использовать в процедуре отбора факторов (на каждом шаге исключается фактор с наименьшим незначимым значением Fxi или tbi).
