Коэффициент эластичности как характеристика силы связи фактора с результатом

Коэффициент эластичности представляет собой показатель силы связи фактора х с результатом у, показывающий, на сколько % изменится значение у при изменении значения фактора на 1 %. Коэффициент эластичности рассчитывается как относительное изменение у на единицу относительного изменения х:

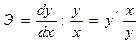Различают обобщающие (средние) и точечные коэффициенты эластичности.

Обобщающий коэффициент эластичности рассчитывается для среднего значения :

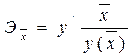и показывает, на сколько % изменится у относительно своего среднего уровня при росте х на 1 % относительно своего среднего уровня.

Точечный коэффициент эластичности рассчитывается для конкретного значения х = х ₀:

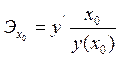и показывает, на сколько % изменится у относительно уровня у (х ₀) при увеличении х на 1 % от уровня х ₀.

В зависимости от вида зависимости между х и у формулы расчета коэффициентов эластичности будут меняться. Основные формулы приведем в таблице.

Вид функции y(x)	Точечный коэффициент Э_хо	Средний коэффициент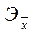
Линейная,	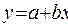Э_хо=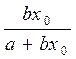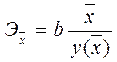
Парабола,	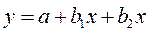Э_хо =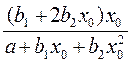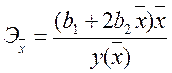
Гипербола,	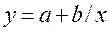Э_хо =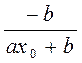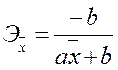
Степенная,	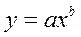Э_хо = b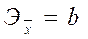
Показательная,	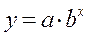Э_хо =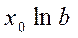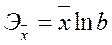

Только для степенных функций 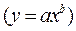коэффициент эластичности представляет собой постоянную независимую от х величину. Именно поэтому степенные функции широко используются в эконометрических исследованиях. Параметр b в таких функциях имеет четкую экономическую интерпретацию – он показывает процентное изменение результата при увеличении фактора на 1 %. Так, если зависимость спроса у от цен х характеризуется уравнением вида: 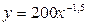, то, следовательно, с увеличением цен на 1 % спрос снижается в среднем на 1,5 %.

Несмотря на широкое использование в эконометрике коэффициентов эластичности, возможны случаи, когда их расчет экономического смысла не имеет. Это происходит тогда, когда для рассматриваемых признаков бессмысленно определение изменения значений в %. Например, бессмысленно определять, на сколько % изменится заработная плата с ростом возраста рабочего на 1 %. В такой ситуации степенная функция, даже если она оказывается наилучшей по формальным соображениям (исходя из наибольшего R²), не может быть экономически интерпретирована.

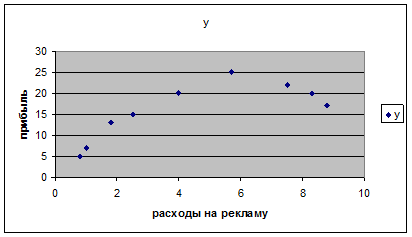
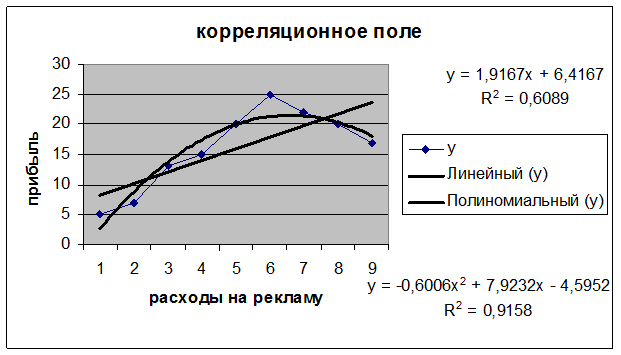
Пример 1. Анализируется прибыль предприятия Y в зависимости от расходов на рекламу Х. По наблюдениям за 9 лет получены следующие данные:

Y
X	8,8	1,0	1,8	2,5	4,0	5,7	7,5	8,3	8,8

а) постройте корреляционное поле и выдвиньте предположение о формуле зависимости между рассматриваемыми показателями;

б) оцените по МНК коэффициенты линейной регрессии и оцените качество построенной регрессии;

в) оцените по МНК коэффициенты квадратичной регрессии и оцените её качество.

Какую из моделей вы предпочтете?

Решение

1) Построим поле корреляции, используя «Мастер диаграмм»

2) Построим уравнение линейной регрессии .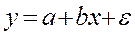

ВЫВОД ИТОГОВ

Регрессионная статистика
Множественный R	0,751709
R-квадрат	0,565066
Нормированный R-квадрат	0,502933
Стандартная ошибка	4,742604
Наблюдения

Дисперсионный анализ
	df	SS	MS	F	Значимость F
Регрессия		204,554	204,554	9,094402	0,019505
Остаток		157,446	22,49229
Итого

	Коэффициенты	Стандартная ошибка	t-статистика	P-Значение	Нижние 95%	Верхние 95%	Нижние 95,0%
Y-пересечение	8,859876	2,846918	3,112094	0,017031	2,127985	15,59177	2,127985
x	1,590622	0,527448	3,015693	0,019505	0,343405	2,837839	0,343405

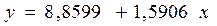
Средняя ошибка аппроксимации составит 30,9 % > 8-10 %.

3) Построим уравнение квадратичной зависимости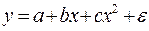

ВЫВОД ИТОГОВ

Регрессионная статистика
Множественный R	0,992323
R-квадрат	0,984706
Нормированный R-квадрат	0,979607
Стандартная ошибка	0,960608
Наблюдения

Дисперсионный анализ
	df	SS	MS	F	Значимость F
Регрессия		356,4634	178,2317	193,149	3,58E-06
Остаток		5,536609	0,922768
Итого

	Коэффициенты	Стандартная ошибка	t-статистика	P-Значение	Нижние 95%	Верхние 95%	Нижние 95,0%
Y-пересечение	-0,98655	0,959919	-1,02774	0,343709	-3,33538	1,362291	-3,33538
x	8,470654	0,546761	15,49244	4,58E-06	7,132779	9,808529	7,132779
x^2	-0,7221	0,05628	-12,8306	1,38E-05	-0,85982	-0,58439	-0,85982

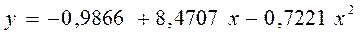
Средняя ошибка аппроксимации составит 4,5 % < 8-10 %.

4) Проведём оценку существенности различий R², вычисленных по одним и тем же исходным данным, через t – критерий Стьюдента:

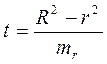где :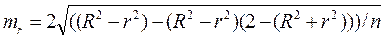

, , , , .

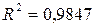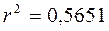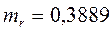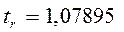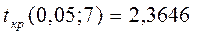Т.к. t_набл < t_кр, то различия между рассматриваемыми показателями корреляции несущественны и, следовательно, возможно применение линейной регрессии.

Вывод: лучшим уравнением по совокупности показателей является квадратичная регрессия.

Замечание. Мастер диаграмм. Тип – точечная. Диаграмма – добавить линию тренда…

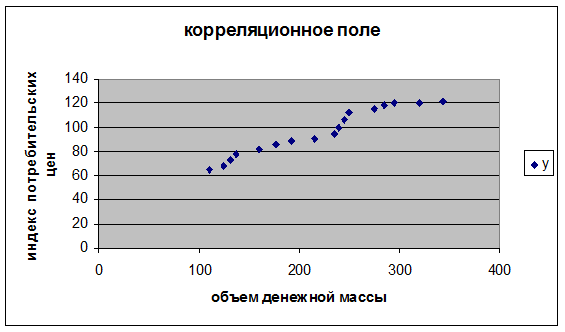
Пример 2. Анализируется индекс потребительских цен Y по объему денежной массы Х на основании данных с 1981 по 1997 год. Необходимо:

1) построить корреляционное поле;

2) построить регрессии: У на Х; Y на lnX; lnY на Х; lnY на lnX;

3) проинтерпретировать коэффициенты регрессии для каждой из моделей;

4) по каждой из моделей определить эластичность Y по Х;

5) определить целесообразность выбора предложенных моделей.

Решение

1) построим корреляционное поле

2) строим уравнения всех регрессий:

ВЫВОД ИТОГОВ

Регрессионная статистика
Множественный R	0,976836
R-квадрат	0,954209
Нормированный R-квадрат	0,951157
Стандартная ошибка	4,313545
Наблюдения

Дисперсионный анализ
	df	SS	MS	F	Значимость F
Регрессия		5816,018	5816,018	312,5771	1,87E-11
Остаток		279,1	18,60667
Итого		6095,118

	Коэффициенты	Стандартная ошибка	t-статистика	P-Значение	Нижние 95%	Верхние 95%
Y-пересечение	38,01618	3,464674	10,97251	1,45E-08	30,6314	45,40095
x	0,265648	0,015025	17,67985	1,87E-11	0,233622	0,297674

ВЫВОД ИТОГОВ

Регрессионная статистика
Множественный R	0,976831
R-квадрат	0,954198
Нормированный R-квадрат	0,951144
Стандартная ошибка	4,314076
Наблюдения

Дисперсионный анализ
	df	SS	MS	F	Значимость F
Регрессия		5815,949	5815,948851	312,4964	1,87E-11
Остаток		279,1688	18,61125308
Итого		6095,118

	Коэффициенты	Стандартная ошибка	t-статистика	P-Значение	Нижние 95%	Верхние 95%
Y-пересечение	-192,679	16,38698	-11,75805947	5,71E-09	-227,607	-157,751
lnx	54,16123	3,06384	17,67756659	1,87E-11	47,63081	60,69165

ВЫВОД ИТОГОВ

Регрессионная статистика
Множественный R	0,972099
R-квадрат	0,944976
Нормированный R-квадрат	0,941308
Стандартная ошибка	0,050994
Наблюдения

Дисперсионный анализ
	df	SS	MS	F	Значимость F
Регрессия		0,669884	0,669884	257,6084	7,44E-11
Остаток		0,039006	0,0026
Итого		0,70889

	Коэффициенты	Стандартная ошибка	t-статистика	P-Значение	Нижние 95%	Верхние 95%
Y-пересечение	3,921623	0,040959	95,74539	2,54E-22	3,834321	4,008924
x	0,002851	0,000178	16,05018	7,44E-11	0,002472	0,00323

ВЫВОД ИТОГОВ

Регрессионная статистика
Множественный R	0,983605
R-квадрат	0,967479
Нормированный R-квадрат	0,965311
Стандартная ошибка	0,039204
Наблюдения

Дисперсионный анализ
	df	SS	MS	F	Значимость F
Регрессия		0,685836	0,685836444	446,2417	1,43E-12
Остаток		0,023054	0,001536917
Итого		0,70889

	Коэффициенты	Стандартная ошибка	t-статистика	P-Значение	Нижние 95%	Верхние 95%
Y-пересечение	1,409022	0,148914	9,46196281	1,03E-07	1,091618	1,726425
lnx	0,588151	0,027842	21,1244329	1,43E-12	0,528806	0,647495

3) Составим сводную таблицу

	R^2	F	Значимость F	ta	tb	A	Э
Y на X	0,954209	312,5771	1,87E-11	10,97251	17,67985	3,40%	0,605689
Y на lnX	0,954198	446,2417	1,87E-11	-11,7581	17,67757	3,50%	0,544866
lnY на X	0,944976	257,6084	7,44E-11	95,74539	16,05018	0,04%	0,626711
lnY на lnX	0,967479	446,2417	1,43E-12	9,461963	21,12443	0,03%	0,588151

Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:

1 2 3

Полупроводниковые приборы. Транзисторы

Конституционно-правовые нормы: понятие, особенности и виды

Анализ финансового состояния предприятия

Индукция и дедукция. Анализ и синтез

Анализ актива баланса

Правовое положение сословий в Российском государстве в XVIII веке

Самый сильный аргумент, почему эволюция человека не могла быть