Блок 10. Содержание выборочного наблюдения, ошибки выборочного наблюдения
Модуль 4. Выборочное наблюдение
Мы уже знаем, что если возникает необходимость проведения наблюдения, то оно может проводиться как сплошное наблюдение, когда обследуются все без исключения единицы наблюдения и как несплошное наблюдение, когда обследуется только определенная часть общей совокупности.
Выборочное наблюдение – основной вид из ряда способов несплошного наблюдения. Выборочным называется наблюдение заранее определенного числа единиц совокупности, отобранных в особом порядке. Выборочный метод исследования предполагает получение обобщающих показателей изучаемой совокупности по обследованной ее части. При этом подлежащая исследованию совокупность называется генеральной совокупностью, а отобранная из генеральной совокупности ее часть называется выборочной совокупностью.
Выборочный метод позволяет при минимальной численности обследуемых единиц получить объективные характеристики всей изучаемой совокупности. Это особенно актуально в современных условиях, когда сплошные наблюдения дороги и не всегда эффективны. Теория и опыт показали, что при правильной организации выборочного наблюдения можно получить достоверные данные о изучаемой совокупности. Эти данные (абсолютные и относительные) достаточно точно воспроизводят – репрезентируют всю совокупность. Выборочные наблюдения практикуются во всех видах социальной и экономической деятельности.
Для более глубокого изучения выборочного метода введем некоторые условные обозначения:
N – объем генеральной совокупности – число входящих в нее единиц;
n - объем выборочной совокупности – число единиц, попавших в выборку;
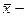 генеральная средняя – среднее значение изучаемого признака в генеральной совокупности;
генеральная средняя – среднее значение изучаемого признака в генеральной совокупности;
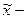 выборочная средняя – среднее значение изучаемого признака в выборочной совокупности;
выборочная средняя – среднее значение изучаемого признака в выборочной совокупности;
р - генеральная доля – доля единиц, обладающих данным признаком в генеральной совокупности;
w - выборочная доля – доля единиц, обладающих данным признаком в выборочной совокупности; 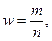 где m- число единиц, обладающих изучаемым признаком,
где m- число единиц, обладающих изучаемым признаком,  n – объем выборочной совокупности;
n – объем выборочной совокупности;
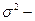 генеральная дисперсия - дисперсия изучаемого признака в генеральной совокупности;
генеральная дисперсия - дисперсия изучаемого признака в генеральной совокупности;
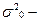 выборочная дисперсия – дисперсия изучаемого признака в выборочной совокупности;
выборочная дисперсия – дисперсия изучаемого признака в выборочной совокупности;
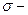 среднее квадратическое отклонение изучаемого признака в генеральной совокупности;
среднее квадратическое отклонение изучаемого признака в генеральной совокупности;
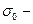 среднее квадратическое отклонение изучаемого признака в выборочной совокупности.
среднее квадратическое отклонение изучаемого признака в выборочной совокупности.
При любом наблюдении (сплошном и несплошном) возникают ошибки при регистрации единиц наблюдения. Такие ошибки называются ошибками регистрации. Они могут быть случайными и систематическими, это связано в значительной степени с субъективным фактором, который всегда присутствует при организации и проведении наблюдения.
При проведении выборочных наблюдений, помимо ошибок регистрации, возникают случайные ошибки репрезентативности (представительности), которые возникают в связи с тем, что отобранная для наблюдения часть общей совокупности имеет отличную от генеральной n
Научным обоснованием случайных ошибок выборки являются теория вероятностей и ее предельные теоремы. Используются теоремы русских математиков П.Л. Чебышева и А.М. Ляпунова. В соответствии с этими теоремами, с увеличением численности выборки размеры случайных ошибок сокращаются, что при достаточно большом объеме выборки случайная ошибка будет сколь угодно мала и что характеристики выборочного наблюдения будут надлежащим образом представлять генеральную совокупность.
Возможные расхождения между характеристиками выборочной и генеральной совокупности измеряются средней ошибкой выборки 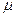 . Под средней ошибкой выборки понимают расхождение между средними выборочной и генеральной совокупности (
. Под средней ошибкой выборки понимают расхождение между средними выборочной и генеральной совокупности (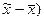 , которое не превышает
, которое не превышает 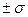 . В математической статистике доказано, что значение средней ошибки выборки определяются по формуле:
. В математической статистике доказано, что значение средней ошибки выборки определяются по формуле:
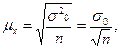 где
где 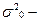 дисперсия изучаемого признака х в выборочной совокупности, а n – численность выборочной совокупности.
дисперсия изучаемого признака х в выборочной совокупности, а n – численность выборочной совокупности.
Соответственно для расчета средней ошибки доли изучаемого признака используется формула:
 где pq – где дисперсия доли изучаемого признака, а n – численность выборочной совокупности. Следовательно, для уменьшения средней ошибки выборки в 3 раза необходимо увеличить объем выборки в 9 раз.
где pq – где дисперсия доли изучаемого признака, а n – численность выборочной совокупности. Следовательно, для уменьшения средней ошибки выборки в 3 раза необходимо увеличить объем выборки в 9 раз.
Рассмотрим условный пример. Генеральная совокупность – число сделок N =1000
Доходность сделок (тыс. руб.) Число сделок
12 200
14 500
15 300
Всего: 1000
Средня доходность:
 тыс. руб.
тыс. руб.
Дисперсия: 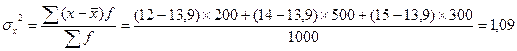
Доля сделок с доходностью 14 и более тыс. рублей р =
 или 80%
или 80%
Предположим, что случайным образом отобрана информация о 200 сделках и получены данные о средних и относительных показателях:
Доходность сделок (тыс. руб.) Число сделок
12 34
14 100
15 66
Всего: 200
Средняя доходность 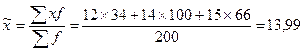 тыс. руб.
тыс. руб.
Дисперсия 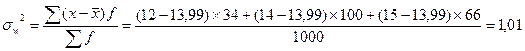
Доля сделок с доходностью 14 и более тыс. рублей w =
 или 83%.
или 83%.
Сведем полученные показатели в таблицу:
|
Теперь можно определить среднюю ошибку выборки:
Для средней доходности 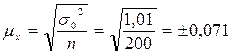 ;
;
Для доли 14 и более т. руб.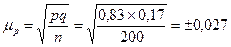 .
.
 2014-02-02
2014-02-02 556
556








