.
Для оценки тесноты связи применяются показатели вариации:
1. Общая дисперсия результативного признака 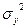 - отражает совокупное влияние факторов:
- отражает совокупное влияние факторов:
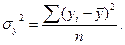
2. Факторная дисперсия результативного признака 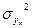 - отражает вариацию только от воздействия изучаемого фактора х:
- отражает вариацию только от воздействия изучаемого фактора х:
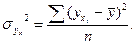
Характеризует колеблемость выравненных значений ух от общей средней величины 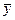 .
.
3. Остаточная дисперсия 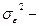 отображает вариацию результативного признака у от всех прочих, кроме х факторов:
отображает вариацию результативного признака у от всех прочих, кроме х факторов:
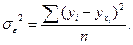
Соотношение между факторной 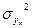 и общей
и общей 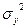 отражает меру тесноты связи между х и у.
отражает меру тесноты связи между х и у.
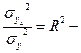 индекс детерминации – доля факторной дисперсии в общей дисперсии. Если это выражение представить как
индекс детерминации – доля факторной дисперсии в общей дисперсии. Если это выражение представить как 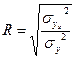 , то R это будет индекс корреляции.
, то R это будет индекс корреляции.
На основе правила сложения дисперсий (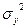 =
=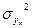 +
+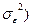 индекс корреляции можно представить как:
индекс корреляции можно представить как: 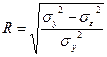 или
или 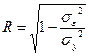 . Индекс корреляции применяется для оценки тесноты связи при всех формах связи.
. Индекс корреляции применяется для оценки тесноты связи при всех формах связи.
Для измерения тесноты линейной связи применяется линейный коэффициент корреляции:

Качественная оценка тесноты связи показателей дается с помощью шкалы Чеддока:
| Показатели тесноты связи | 0,1-0,3 | 0,3-0,5 | 0,5-0,7 | 0,7-0,9 | 0,9-0,99 |
| Характеристика силы связи | слабая | умеренная | заметная | высокая | весьма высокая |
Рассмотрим на условном примере применение регрессионно-корреляционного анализа связи парной корреляции. Имеется выборочная информация о работе 8 гостиниц, у которых различная среднегодовая наполняемость гостиничных номеров и различная рентабельность их деятельности. В результате регрессионно-корреляционного анализа необходимо определить, существует ли прямая зависимость между наполняемостью гостиничных номеров и если она есть, то насколько она тесная:
| N пп | Наполняе-мость (в %%) х | Рентабель- ность (в %%) у | х2 | у2 | ху | Выравненное (теоретическое) ух |
| 8,2 7,0 9,3 8,1 9,5 10,5 7,5 6,3 | 67,24 49,00 86,49 65,61 90,25 110,25 56,25 39,69 | 492,0 364,0 669,6 526,5 712,5 840,0 420,0 315,0 | 7,61 6,65 9,05 8,21 9,41 10,01 7,13 6,41 | |||
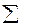 | 66,4 | 564,78 | 4339,6 | 64,48 |
Определим параметры уравнения линейной парной регрессии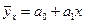 :
:
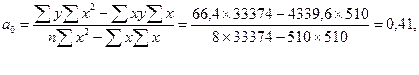
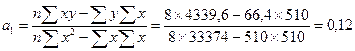 .
.
Наше уравнение парной регрессии будет иметь вид: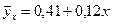 . Подставим в это уравнение эмпирические значения х и рассчитаем теоретические значения
. Подставим в это уравнение эмпирические значения х и рассчитаем теоретические значения  7,61 и т. д.
7,61 и т. д.
Теперь определим тесноту связи между наполняемостью гостиниц и рентабельностью их деятельности:
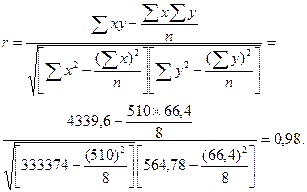
В результате проведенного анализа установлено, что между наполняемостью гостиниц и рентабельностью их деятельности существует прямая весьма высокая зависимость.
На практике часто возникает необходимость произвести оценку близости эмпирических частот к теоретическим. Такую оценку можно произвести с помощью критериев близости, называемых критериями согласия. Наиболее часто применяется для этих целей – критерий согласия Пирсона  («хи»- квадрат), который рассчитывается по формуле:
(«хи»- квадрат), который рассчитывается по формуле:
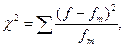
где f – эмпирические частоты,
Оценка близости эмпирических частот к теоретическим определяется по вероятности достижения  данной величины Р(
данной величины Р( ) при случайных отклонениях частот. Если вероятность Р(
) при случайных отклонениях частот. Если вероятность Р( ) значительно отличается от нуля (больше, чем 0,05), то отклонения эмпирических частот от теоретических можно считать случайными. Если Р(
) значительно отличается от нуля (больше, чем 0,05), то отклонения эмпирических частот от теоретических можно считать случайными. Если Р( )< 0,05, то отклонения нельзя считать случайными, а эмпирическое и теоретические распределения
)< 0,05, то отклонения нельзя считать случайными, а эмпирическое и теоретические распределения  принципиально друг от друга отличаются.
принципиально друг от друга отличаются.
Величина  зависит не только от отклонений фактических частот от теоретических, но и от количества групп, на которые разбита совокупность, поэтому таблицы критических значений
зависит не только от отклонений фактических частот от теоретических, но и от количества групп, на которые разбита совокупность, поэтому таблицы критических значений  рассчитаны для различных степеней свободы варьирования эмпирических частот (приложение). Для нормального распределения число степеней свободы К=n-3, где n – число групп.
рассчитаны для различных степеней свободы варьирования эмпирических частот (приложение). Для нормального распределения число степеней свободы К=n-3, где n – число групп.
Рассмотрим и оценим на примере близость эмпирических и теоретических распределений. Турфирма в течение месяца реализовала 50 путевок. Объем дневной реализации путевок распределился следующим образом (табл.7):
Таблица 7
| Число путевок, реализуемых в течение дня | Фактическая реализация f | Теоретическая реализация  | f- 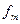 | (f- 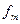 )2 )2 | 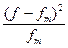 |
| до 3 7 и более | -5 -1 | 0,25 0,75 0,22 2,08 0,25 | |||
| Всего: | - | - | 3,55 |
Таким образом:  К=5-3=2.
К=5-3=2.
По таблице критических значений  (приложение) определяем вероятность Р(
(приложение) определяем вероятность Р(
 , что значительно превышает 0,05. Это означает, что отклонения фактических частот от эмпирических можно считать случайными, а само распределение реализации путевок близко к нормальному распределению.
, что значительно превышает 0,05. Это означает, что отклонения фактических частот от эмпирических можно считать случайными, а само распределение реализации путевок близко к нормальному распределению.
Приложение 1
 2014-02-02
2014-02-02 730
730








