Рассмотрим формулу бинома Ньютона.
Бином Ньютона (1+ x) n, после раскрытия скобок и приведения подобных, преобразуется в многочлен канонического вида a 0 xn + a 1 xn -1+…+ an -1 x 1+ anx 0, где a 0=1, an =1, x 0=1. Оказывается, что 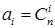 , где i =0,1,…, n. Поэтому числа сочетаний
, где i =0,1,…, n. Поэтому числа сочетаний 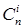 называются также биномиальными коэффициентами. Применятся обозначение:
называются также биномиальными коэффициентами. Применятся обозначение: 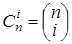 . Формула в следующей теореме называется формулой бинома Ньютона или биномом Ньютона.
. Формула в следующей теореме называется формулой бинома Ньютона или биномом Ньютона.
Теорема. 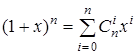 .
.
Доказательство. 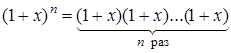 . Раскроем скобки и приведем подобные: в полученном многочлене коэффициент при степени xi равен сумме i единиц и n -i нулей. Число всевозможных выборов i единиц из общего числа выборов n равно
. Раскроем скобки и приведем подобные: в полученном многочлене коэффициент при степени xi равен сумме i единиц и n -i нулей. Число всевозможных выборов i единиц из общего числа выборов n равно 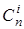 .
.
Следствие. 1) 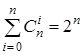 ;2)
;2) 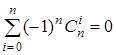 ;3)
;3) 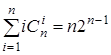 ;
;
4) 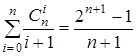 .
.
Доказательство. 1) В тождестве теоремы подставим x =1.
2) В том же тождестве подставим x =-1.
3) Продифференцируем обе части того же тождества по x:
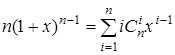 .
.
Затем подставим x =1.
4) Проинтегрируем обе части того же тождества по x от 0 до 1:
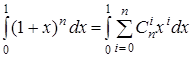 .
.
Получим: 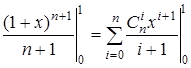 .
.
 2014-02-02
2014-02-02 1600
1600








