Рекуррентная формула для числа сочетаний без повторений

Используя формулу для числа сочетаний без повторений, можно доказать следующую теорему.

Теорема. , , .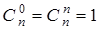

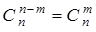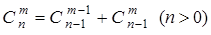Доказательство. . .

.

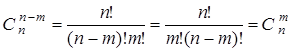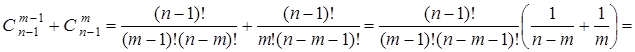
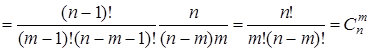Пример. Найти все биномиальные коэффициенты для .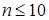

Решение запишем в виде треугольника Паскаля – бесконечной таблицы, имеющей треугольную форму. В этом треугольнике на вершине и по бокам стоят единицы, так как 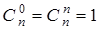. Каждое внутреннее число равно сумме двух расположенных над ним чисел: 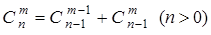. Строки треугольника симметричны относительно вертикальной оси: .

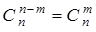Биномиальный коэффициент 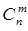лежит на пересечении строки n и столбца m.