Дерево – это граф, в котором выполняются любые два условия из трех условий следующей теоремы.
Теорема. Пусть для (p, q)-графа G рассматриваются три условия:
(1) G – связный граф;
(2) G – ациклический граф;
(3) p = q +1.
Тогда каждое из условий (1) – (3) следует из двух других.
Доказательство. (1), (2) Þ (3). Докажем методом математической индукции по числу ребер q. При q =1 и q =2 утверждение теоремы легко проверить. Если q ³3, то удалим одно из серединных ребер. Тогда граф G разбивается на 2 подграфа – (p 1, q 1)-граф G 1 и (p 2, q 2)-граф G 2, p = p 1+ p 2, q = q 1+ q 2+1. Так как q 1< q, q 2< q, то по индуктивному предположению, p 1= q 1+1, p 2= q 2+1, откуда p = p 1+ p 2= q 1+1+ q 2+1=(q 1+ q 2+1)+1= q +1.
(1), (3) Þ (2). Докажем методом от противного. Допустим, что граф G содержит цикл с s вершинами и с s ребрами. Каждый из оставшихся p - s вершин присоединяется к этому циклу или к ранее присоединенному ребру "новым", "своим" ребром. Получается, что q не меньше суммы s +(p - s)= p, что противоречит условию (3). Значит, граф G не содержит циклов.
(2), (3) Þ (1). Докажем методом от противного. Допустим, что граф G состоит из k компонент связности(k ³1). Каждая из них будет связным ациклическим графом G 1, …, Gk, соответственно с p 1,…, pk вершинами и q 1,…, qk ребрами, p = p 1+…+ pk, q = q 1+…+ qk. Для графов G 1, …, Gk имеем k равенств: p 1= q 1+1, …, pk = qk +1. Отсюда p = p 1+…+ pk =(q 1+1)+…+(pk +1)= q + k, что противоречит условию (3). Значит, граф G связный.
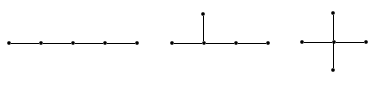
Пример. Деревья с числом вершин не больше 5. Приведем все попарно неизоморфные деревья с числом вершин, не больше 5:

 2014-02-02
2014-02-02 1792
1792







