Обнаружение гетероскедастичности

Не существует какого-либо однозначного метода определения гетероскедастичности. При этом разработано большое число различных тестов и критериев. Рассмотрим наиболее популярные из них.

3.1. Тест ранговой корреляции Спирмена. Выдвигается Ho об отсутствии гетероскедастичности случайного члена. Предполагается, что дисперсия случайного члена будет либо увеличиваться, либо уменьшаться по мере увеличения Х, и поэтому в регрессии по МНК абсолютные величины остатков 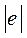и значения Х будут коррелированны. Схема теста:

1) данные по Х и остатки 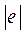ранжируются по Х и определяются их ранги;

2) коэффициент ранговой корреляции Спирмена определяется по формуле

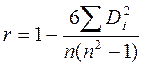, где Di - разность между рангами Х и ;

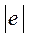3) Статистический критерий имеет распределение Стьюдента, т.к. .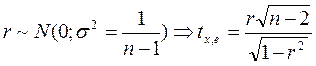

Если 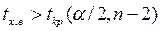, H₀ об отсутствии гетероскедастичности будет отклонена.

Если в модели регрессии имеется более одной объясняющей переменной, то проверка гипотезы может выполняться с использованием любой из них.

Пример. Исследуется зависимость между доходом (Х) домохозяйства и его расходом (Y) на продукты питания. Выборочные данные по 40 домохозяйствам даны в таблице.

x	25,5	26,5	27,2	29,6	35,7	38,6		39,3		41,9
y	14,5	11,3	14,7	10,2	13,5	9,9	12,4	8,6	10,3	13,9

x	42,5	44,2	44,8	45,5	45,5	48,3	49,5	52,3	55,7
y	14,9	11,6	21,5	10,8	13,8		18,2	19,1	16,3	17,5

x		61,7	62,5	64,7	69,7	71,2	73,8	74,7	75,8	76,9
y	10,9	16,1	10,5	10,6		8,2	14,3	21,8	26,1

x	79,2	81,5	82,4	82,8		85,9	86,4	86,9	88,3
y	19,8	21,2		17,3	23,5		18,3	13,7	14,5	27,3

Решение

1. Строим уравнение регрессии и определяем остатки.

ВЫВОД ИТОГОВ

Регрессионная статистика
Множественный R	0,564649
R-квадрат	0,318828
Нормированный R-квадрат	0,300903
Стандартная ошибка	4,672041
Наблюдения

Дисперсионный анализ
	df	SS	MS	F	Значимость F
Регрессия		388,2371	388,2371	17,786	0,0001
Остаток		829,4627	21,82796
Итого		1217,7

	Коэффициенты	Стандартная ошибка	t-статистика	P-Значение	Нижние 95%	Верхние 95%	Нижние 95,0%	Верхние 95,0%
Y-пересечение	7,040019	2,322793	3,030842	0,0044	2,3378	11,742	2,3378	11,74
х	0,156883	0,037199	4,217372	0,0001	0,0816	0,2322	0,0816	0,232

ВЫВОД ОСТАТКА

Наблюдение	Предсказанное у	Остатки
	11,04054	3,459461
	11,19742	0,102578
	11,30724	3,39276
	11,68376	-1,48376
	12,64075	0,859253
	13,09571	-3,19571
	13,15846	-0,75846
	13,20553	-4,60553
	13,31534	-3,01534
	13,61342	0,286578
	13,70755	1,192448
	13,97425	-2,37425
	14,06838	7,431617
	14,1782	-3,3782
	14,1782	-0,3782
	14,61747	1,382526
	14,80573	3,394266
	15,24501	3,854994
	15,77841	0,521591
	16,29612	1,203877
	16,60989	-5,70989
	16,71971	-0,61971
	16,84521	-6,34521
	17,19036	-6,59036
	17,97477	11,02523
	18,2101	-10,0101
	18,61799	-4,31799
	18,75919	3,040812
	18,93176	7,16824
	19,10433	0,895669
	19,46516	0,334838
	19,82599	1,374006
	19,96719	9,032812
	20,02994	-2,72994
	20,06132	3,438682
	20,51628	1,483721
	20,59472	-2,29472
	20,67316	-6,97316
	20,8928	-6,3928
	21,00262	6,297383

2. Значения х_i уже упорядочены по возрастанию, поэтому определяем ранги х_i и ранги соответствующих остатков.

х	ABS(e)	ранг х	ранг е	D
25,5	3,459461			-25
26,5	0,102578
27,2	3,39276			-20
29,6	1,48376			-11
35,7	0,859253			-3
38,6	3,195708			-15
	0,758461
39,3	4,605526			-21
	3,015344			-10
41,9	0,286578
42,5	1,192448
44,2	2,374253			-5
44,8	7,431617			-24
45,5	3,378201			-8
45,5	0,378201
48,3	1,382526
49,5	3,394266			-7
52,3	3,854994			-9
55,7	0,521591
	1,203877
	5,70989			-9
61,7	0,619708
62,5	6,345214			-9
64,7	6,590357			-10
69,7	11,02523			-15
71,2	10,0101			-13
73,8	4,317994			-1
74,7	3,040812
75,8	7,16824			-7
76,9	0,895669
79,2	0,334838
81,5	1,374006
82,4	9,032812			-5
82,8	2,729942
	3,438682
85,9	1,483721
86,4	2,294721
86,9	6,973162
88,3	6,392799
	6,297383

3. Определяем коэффициент корреляции Спирмена и t-статистику

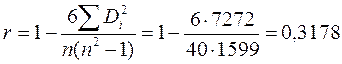
4. Т.к. t_кр(0,05;38)=2,021 < 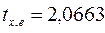, то гетероскедастичность доказана.

3.2. Метод Голдфелда-Квандта. При проведении проверки по этому тесту предполагается, что стандартное отклонение 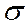случайного члена пропорционально значению независимой переменной Х. Схема теста:

1) все n наблюдений упорядочиваются по возрастанию переменной Х;

2) оцениваются отдельные регрессии для первых m и для последних m наблюдений. Средние (n-2m) наблюдений отбрасываются ();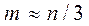

3) составляется статистика 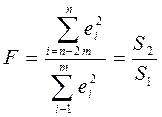, где S₁, S₂ – суммы квадратов остатков для первых и последних наблюдений;

4) Если 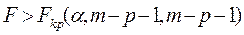, Ho об отсутствии гетероскедастичности отклоняется (если обратно пропорционально Х, то ).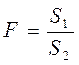

Пример. Воспользуемся условием предыдущего примера и определим наличие гетероскедастичности остатков с помощью теста Голдфелда-Квандта.

Решение.

1) Упорядоченные по возрастанию х данные х_i и у_i разбиваются на три приблизительно равные части. Для первой и последней строятся уравнения регрессии и рассчитывается F-статистика.

1-я часть 2-я часть


х	у	x	y
25,5	14,5	73,8	14,3
26,5	11,3	74,7	21,8
27,2	14,7	75,8	26,1
29,6	10,2	76,9
35,7	13,5	79,2	19,8
38,6	9,9	81,5	21,2
	12,4	82,4
39,3	8,6	82,8	17,3
	10,3		23,5
41,9	13,9	85,9
42,5	14,9	86,4	18,3
44,2	11,6	86,9	13,7
44,8	21,5	88,3	14,5
45,5	10,8		27,3

ВЫВОД ИТОГОВ

Регрессионная статистика
Множественный R	0,11
R-квадрат	0,012
Нормированный R-квадрат	-0,07
Стандартная ошибка	3,335
Наблюдения

Дисперсионный анализ
	df	SS	MS	F	Значимость F
Регрессия		1,6285	1,628	0,146	0,7087
Остаток		133,5	11,12
Итого		135,12

	Коэффициенты	Стандартная ошибка	t-статистика	P-Значение	Нижние 95%	Верхние 95%	Нижние 95,0%	Верхние 95,0%
Y-пересечение	10,87	4,926	2,206	0,048	0,1351	21,6	0,135078	21,60065
х	0,05	0,1304	0,383	0,709	-0,234	0,334	-0,23415	0,3339

ВЫВОД ИТОГОВ

Регрессионная статистика
Множественный R	0,039
R-квадрат	0,002
Нормированный R-квадрат	-0,082
Стандартная ошибка	4,992
Наблюдения

Дисперсионный анализ
	df	SS	MS	F	Значимость F
Регрессия		0,4598	0,46	0,018	0,8942
Остаток		299,09	24,92
Итого		299,55

	Коэффициенты	Стандартная ошибка	t-статистика	P-Значение	Нижние 95%	Верхние 95%	Нижние 95,0%	Верхние 95,0%
Y-пересечение	23,63	22,15	1,067	0,307	-24,63	71,89	-24,6287	71,89183
x	-0,037	0,27	-0,136	0,894	-0,625	0,552	-0,62485	0,551522

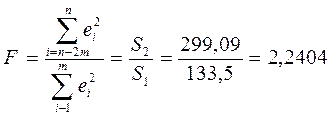
2) Т.к. 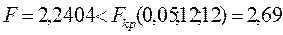, то нет оснований отвергать Н₀ об отсутствии гетероскедастичности.

3.3. Тест Глейзера. Тест Глейзера основывается на более общих представлениях о зависимости стандартной ошибки случайного члена от значений объясняющей переменной. Предположение о пропорциональности 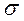и Х снимаем и хотим проверить, может ли быть более подходящей какая-либо другая функциональная форма, например, . Чтобы использовать этот метод:

1) оценивают регрессию Y по Х и вычисляют 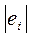– абсолютные значения остатков;

2) оценивают регрессию 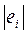по 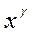для нескольких значений : ;

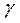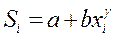3) если Н₀: b = 0 отклоняется (т.е. b значим), то гипотеза об отсутствии гетероскедастичности будет отклонена.

Если при оценивании более чем одной функции получается значимая оценка b, то ориентиром при определении характера гетероскедастичности может служить лучшая из них.

Пример. Воспользуемся расчетами предыдущего примера и проверим наличие гетероскедастичности с помощью теста Глейзера.

Решение

1) Рассчитаем уравнения регрессии е_i от 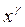при .

х	ABS(e)	x^(-1)	x^(-0,5)	x^0,5	x^1,5
25,5	3,459461	0,039216	0,19803	5,049752	128,7687
26,5	0,102578	0,037736	0,194257	5,147815	136,4171
27,2	3,39276	0,036765	0,191741	5,215362	141,8578
29,6	1,48376	0,033784	0,183804	5,440588	161,0414
35,7	0,859253	0,028011	0,167365	5,974948	213,3056
38,6	3,195708	0,025907	0,160956	6,21289	239,8175
	0,758461	0,025641	0,160128	6,244998	243,5549
39,3	4,605526	0,025445	0,159516	6,268971	246,3706
	3,015344	0,025	0,158114	6,324555	252,9822
41,9	0,286578	0,023866	0,154487	6,473021	271,2196
42,5	1,192448	0,023529	0,153393	6,519202	277,0661
44,2	2,374253	0,022624	0,150414	6,648308	293,8552
44,8	7,431617	0,022321	0,149404	6,69328	299,859
45,5	3,378201	0,021978	0,14825	6,745369	306,9143
45,5	0,378201	0,021978	0,14825	6,745369	306,9143
48,3	1,382526	0,020704	0,143889	6,94982	335,6763
49,5	3,394266	0,020202	0,142134	7,035624	348,2634
52,3	3,854994	0,01912	0,138277	7,231874	378,227
55,7	0,521591	0,017953	0,13399	7,463243	415,7026
	1,203877	0,016949	0,130189	7,681146	453,1876
	5,70989	0,016393	0,128037	7,81025	476,4252
61,7	0,619708	0,016207	0,127309	7,854935	484,6495
62,5	6,345214	0,016	0,126491	7,905694	494,1059
64,7	6,590357	0,015456	0,124322	8,043631	520,4229
69,7	11,02523	0,014347	0,11978	8,348653	581,9011
71,2	10,0101	0,014045	0,118511	8,438009	600,7863
73,8	4,317994	0,01355	0,116405	8,590693	633,9931
74,7	3,040812	0,013387	0,115702	8,642916	645,6258
75,8	7,16824	0,013193	0,114859	8,70632	659,939
76,9	0,895669	0,013004	0,114035	8,769265	674,3564
79,2	0,334838	0,012626	0,112367	8,899438	704,8355
81,5	1,374006	0,01227	0,11077	9,027735	735,7604
82,4	9,032812	0,012136	0,110163	9,077445	747,9814
82,8	2,729942	0,012077	0,109897	9,099451	753,4345
	3,438682	0,012048	0,109764	9,110434	756,166
85,9	1,483721	0,011641	0,107896	9,268225	796,1406
86,4	2,294721	0,011574	0,107583	9,29516	803,1018
86,9	6,973162	0,011507	0,107273	9,322017	810,0833
88,3	6,392799	0,011325	0,106419	9,396808	829,7381
	6,297383	0,011236	0,106	9,433981	839,6243

ВЫВОД ИТОГОВ

Регрессионная статистика
Множественный R	0,347879
R-квадрат	0,12102
Нормированный R-квадрат	0,097889
Стандартная ошибка	2,732943
Наблюдения

Дисперсионный анализ
	df	SS	MS	F	Значимость F
Регрессия		39,07716	39,07716	5,23193	0,027833
Остаток		283,8211	7,468976
Итого		322,8983

	Коэффициенты	Стандартная ошибка	t-статистика	P-Значение	Нижние 95%	Верхние 95%
Y-пересечение	8,7119	2,294002	3,797686	0,000512	4,067936	13,35586
x^(-0,5)	-37,7515	16,50452	-2,28734	0,027833	-71,1631	-4,33981

ВЫВОД ИТОГОВ

Регрессионная статистика
Множественный R	0,35414
R-квадрат	0,125415
Нормированный R-квадрат	0,1024
Стандартная ошибка	2,726101
Наблюдения

Дисперсионный анализ
	df	SS	MS	F	Значимость F
Регрессия		40,49641	40,49641	5,449198	0,024963
Остаток		282,4019	7,431628
Итого		322,8983

	Коэффициенты	Стандартная ошибка	t-статистика	P-Значение	Нижние 95%	Верхние 95%
Y-пересечение	-2,15816	2,486641	-0,8679	0,390897	-7,1921	2,875785
x^0,5	0,754429	0,323186	2,334352	0,024963	0,100174	1,408685

ВЫВОД ИТОГОВ

Регрессионная статистика
Множественный R	0,351385
R-квадрат	0,123472
Нормированный R-квадрат	0,100405
Стандартная ошибка	2,729129
Наблюдения

Дисперсионный анализ
	df	SS	MS	F	Значимость F
Регрессия		39,8688	39,8688	5,35285	0,026194
Остаток		283,0295	7,448144
Итого		322,8983

	Коэффициенты	Стандартная ошибка	t-статистика	P-Значение	Нижние 95%	Верхние 95%
Y-пересечение	0,58244	1,356838	0,429263	0,670156	-2,16433	3,329215
х	0,050274	0,02173	2,313623	0,026194	0,006285	0,094263

ВЫВОД ИТОГОВ

Регрессионная статистика
Множественный R	0,345728
R-квадрат	0,119528
Нормированный R-квадрат	0,096358
Стандартная ошибка	2,735261
Наблюдения

Дисперсионный анализ
	df	SS	MS	F	Значимость F
Регрессия		38,59537	38,59537	5,158668	0,02888
Остаток		284,3029	7,481655
Итого		322,8983

	Коэффициенты	Стандартная ошибка	t-статистика	P-Значение	Нижние 95%	Верхние 95%
Y-пересечение	1,504832	1,002367	1,501278	0,141548	-0,52435	3,534019
x^1,5	0,004324	0,001904	2,27127	0,02888	0,00047	0,008178

ВЫВОД ИТОГОВ

Регрессионная статистика
Множественный R	0,338157
R-квадрат	0,11435
Нормированный R-квадрат	0,091044
Стандартная ошибка	2,743292
Наблюдения

Дисперсионный анализ
	df	SS	MS	F	Значимость F
Регрессия		36,92349	36,92349	4,906351	0,032827
Остаток		285,9748	7,525652
Итого		322,8983

	Коэффициенты	Стандартная ошибка	t-статистика	P-Значение	Нижние 95%	Верхние 95%
Y-пересечение	5,973455	1,173304	5,091141	9,98E-06	3,598226	8,348684
x^(-1)	-124,996	56,43102	-2,21503	0,032827	-239,235	-10,7577

2) Т.к. коэффициент b статистически значим во всех уравнениях, то гетероскедастичность доказана. Наилучший коэффициент детерминации (R² = 0,1254) при 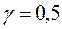, поэтому примем зависимость: 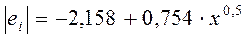(см. далее).

3.4. Тест Парка. Тест относится к формализованным тестам гетероскедастичности. Предполагается, что дисперсия остатков связана со значениями факторов функцией 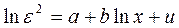. Данная регрессия строится для каждого фактора в условиях многофакторной модели. Проверяется значимость коэффициента регрессии b по t-критерию Стьюдента. Если коэффициент регрессии окажется статистически значимым, то, следовательно, имеет место гетероскедастичность.

Пример. По данным предыдущего примера построим регрессию .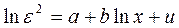

ВЫВОД ИТОГОВ

Регрессионная статистика
Множественный R	0,343033
R-квадрат	0,117672
Нормированный R-квадрат	0,094453
Стандартная ошибка	2,097694
Наблюдения

Дисперсионный анализ
	df	SS	MS	F	Значимость F
Регрессия		22,30024	22,30024	5,067869	0,030238
Остаток		167,2121	4,400319
Итого		189,5124

	Коэффициенты	Стандартная ошибка	t-статистика	P-Значение	Нижние 95%	Верхние 95%
Y-пересечение	-6,49359	3,634358	-1,78672	0,081962	-13,851	0,863782
lnx	2,027965	0,90084	2,251193	0,030238	0,204309	3,851621

Так как коэффициент регрессии статистически значим, то гетероскедастичность доказана.

3.5. Тест Уайта. Предполагается, что дисперсия ошибок регрессии представляет собой квадратичную функцию от значений факторов, т.е. при наличии одного фактора , или при р факторах

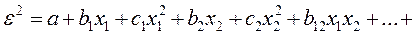
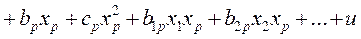О наличии или отсутствии гетероскедастичности остатков судят по величине F-критерия Фишера. Если фактическое значение критерия выше табличного, то, следовательно, существует корреляционная связь дисперсии ошибок от значений факторов, и имеет место гетероскедастичность остатков.

Пример. Определим квадратичную функцию для нашего примера . Пусть х₁= х, х₂ = х², построим уравнение множественной регрессии

ВЫВОД ИТОГОВ

Регрессионная статистика
Множественный R	0,353257
R-квадрат	0,12479
Нормированный R-квадрат	0,077482
Стандартная ошибка	27,61916
Наблюдения

Дисперсионный анализ
	df	SS	MS	F	Значимость F
Регрессия		4024,315	2012,157	2,637794	0,084932
Остаток		28224,27	762,8181
Итого		32248,59

	Коэффициенты	Стандартная ошибка	t-статистика	P-Значение	Нижние 95%	Верхние 95%
Y-пересечение	-38,76	44,00045	-0,8809	0,384058	-127,913	50,39338
х	1,674985	1,618236	1,035069	0,307355	-1,60387	4,953843
х^2	-0,01017	0,013621	-0,74683	0,459886	-0,03777	0,017426