Методы смягчения проблемы гетероскедастичности.
Обнаружение гетероскедастичности.
Суть гетероскедастичности.
Обобщенная линейная модель множественной регрессии. Теорема Айткена.
Обобщенная линейная модель множественной регрессии. Гетероскедастичность.
Лекция 6
Вопросы:
Рассмотрим линейную модель множественной регрессии:
1) 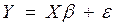
2) 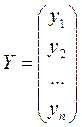 ,
,  ,
, 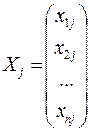 ,
,  ,
, 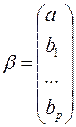
Значения признака Матрица объясняющих Вектор Вектор Вектор
переменных, столбцами регрессора j случайных коэфф-тов
которой являются Xj ошибок регрессии
3)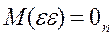 ,
, 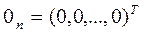
В классической модели компоненты вектора возмущений некоррелированы М(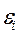
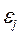 ) = 0 при
) = 0 при 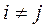 , а дисперсии компонент постоянны
, а дисперсии компонент постоянны 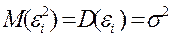 , ковариационная матрица возмущений
, ковариационная матрица возмущений
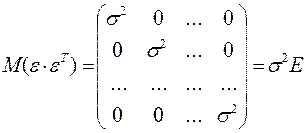
Суть обобщения регрессионной модели состоит в том, что ковариации и дисперсии объясняющих переменных могут быть произвольными (т.о. обобщенная модель множественной регрессии отличается от классической только видом ковариационной матрицы). 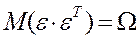 - положительно определенная матрица (АТ = А и хТАх > 0). В классической модели множественной регрессии обычным МНК был получен вектор оценок
- положительно определенная матрица (АТ = А и хТАх > 0). В классической модели множественной регрессии обычным МНК был получен вектор оценок 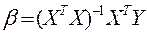 параметров, он является несмещенной и состоятельной оценкой для
параметров, он является несмещенной и состоятельной оценкой для 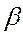 . Рассмотрим ковариационную матрицу
. Рассмотрим ковариационную матрицу
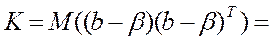
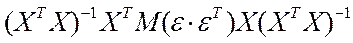
В классической модели 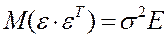 и К =
и К = 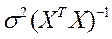 . В качестве выборочной оценки ковариационной матрицы К была взята матрица
. В качестве выборочной оценки ковариационной матрицы К была взята матрица 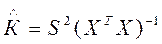 , где
, где 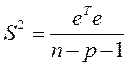 , причем
, причем
M(S2) = 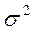 и
и 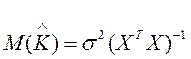 = К, т.е.
= К, т.е. 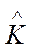 - несмещенная оценка К.
- несмещенная оценка К.
В обобщенной модели 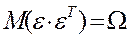 и К =
и К = 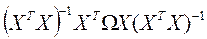 . Если в качестве оценки матрицы К взять ту же матрицу, то
. Если в качестве оценки матрицы К взять ту же матрицу, то 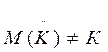 , т.е.
, т.е. 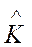 - смещенная оценка для К. Т.о., обычный МНК в обобщенной линейной регрессионной модели дает смещенную оценку ковариационной матрицы К вектора оценок параметров. Следовательно, оценка не будет оптимальной в смысле теоремы Гаусса-Маркова. Для получения наиболее эффективной оценки ковариационной матрицы К нужно использовать оценку, получаемую так называемым обобщенным МНК.
- смещенная оценка для К. Т.о., обычный МНК в обобщенной линейной регрессионной модели дает смещенную оценку ковариационной матрицы К вектора оценок параметров. Следовательно, оценка не будет оптимальной в смысле теоремы Гаусса-Маркова. Для получения наиболее эффективной оценки ковариационной матрицы К нужно использовать оценку, получаемую так называемым обобщенным МНК.
Теорема Айткена: в классе линейных несмещенных оценок вектора 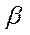 для обобщенной регрессионной модели оценка
для обобщенной регрессионной модели оценка 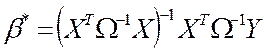 имеет наименьшую ковариационную матрицу.
имеет наименьшую ковариационную матрицу.
Для применения обобщенного МНК надо знать ковариационную матрицу вектора возмущений 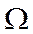 , что встречается крайне редко в практике эконометрического моделирования. Если считать все n(n+1)/2 элементов матрицы
, что встречается крайне редко в практике эконометрического моделирования. Если считать все n(n+1)/2 элементов матрицы 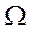 неизвестными параметрами обобщенной модели (в дополнение к (р+1) параметрам регрессии), то общее число параметров превысит число наблюдений n, что сделает оценку этих параметров неразрешимой задачей.
неизвестными параметрами обобщенной модели (в дополнение к (р+1) параметрам регрессии), то общее число параметров превысит число наблюдений n, что сделает оценку этих параметров неразрешимой задачей.
Для практической реализации обобщенного МНК вводятся дополнительные условия на структуру матрицы 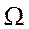 .
.
 2014-02-02
2014-02-02 2328
2328







