Суть гетероскедастичности

В случаях, когда выполняются все предпосылки теоремы Гаусса-Маркова, оценки, полученные по МНК, являются несмещенными, состоятельными и эффективными. Если распределение случайных остатков 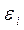не соответствует некоторым предпосылкам МНК, то следует корректировать модель.

Прежде всего, необходимо проверить случайный характер остатков 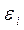. Для этого можно построить график зависимости остатков 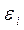от теоретических значений результативного признака 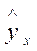(рис.1).

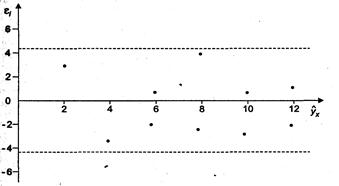
Рис. 1. Зависимость случайных остатков от теоретических значений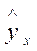

Если на графике нет направленности в расположении точек 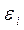, то остатки 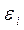представляют собой случайные величины и использование МНК оправдано.

Возможны следующие случаи (рис.2.):

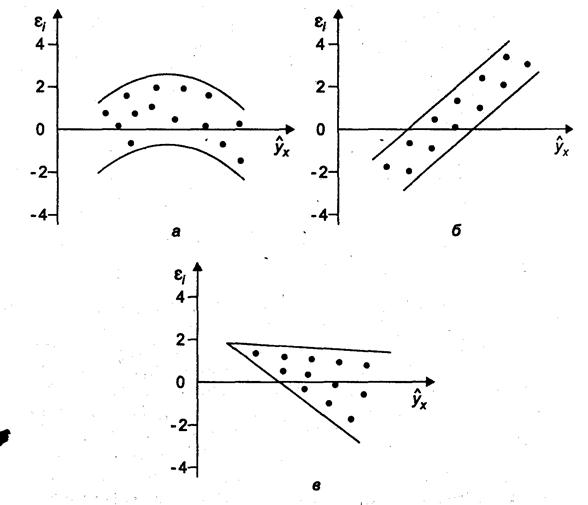
Рис.2. Зависимость 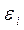от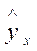

а) остатки не случайны; б) остатки носят систематический характер; в) остатки не имеют постоянной дисперсии.

В этих случаях необходимо использовать другую функцию, либо вводить дополнительную информацию.

Другой предпосылкой регрессионного анализа является предположение о постоянстве дисперсии случайного члена для всех наблюдений (гомоскедастичность).

Это значит, что для каждого значения объясняющей переменной случайные члены имеют одинаковые дисперсии.

D(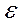) = M(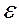²) – M²(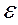) = M(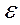²) = 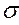² = Const для всех наблюдений.

Если это условие не соблюдается, то имеет место гетероскедастичность (рис. 3).

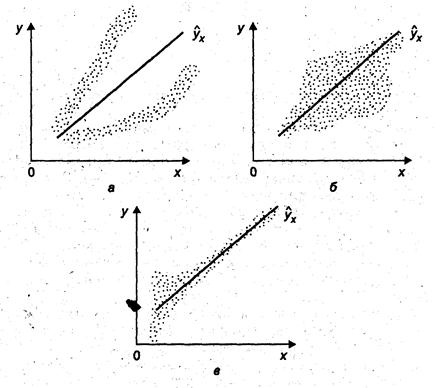
Рис. 3. Примеры гетероскедастичности.

Гомоскедастичность остатков означает, что дисперсия остатков одинакова для каждого значения х (рис. 4, рис. 5).

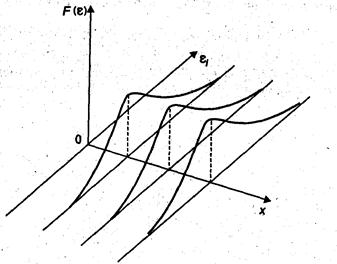
Рис. 4. Гомоскедастичность остатков

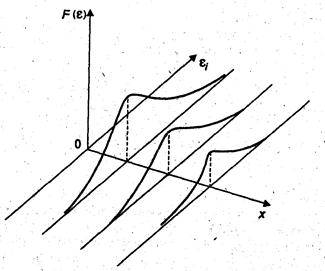
Рис.5. Гетероскедастичность остатков

Наличие гетероскедастичности может привести к смещенности оценок коэффициентов регрессии, хотя несмещенность оценок в основном зависит от соблюдения предположения о независимости остатков и величин факторов (т.е. cov(х,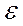) = 0). Гетероскедастичность будет сказываться на уменьшении эффективности оценок параметров. В частности, невозможно использовать формулу стандартной ошибки коэффициентов S_b, предполагающей единую дисперсию остатков. При нарушении гомоскедастичности имеет место неравенство .

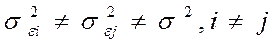Поэтому все выводы, получаемые на основе соответствующих t- и F- статистик, а также интервальные оценки будут ненадежными. Следовательно, статистические выводы будут неверны.

Возможные причины:

1. Значения переменных значительно различаются для разных наблюдений. Например, строя зависимость между государственными расходами на образование и ВВП в различных странах используем и Сингапур, и США, где 3% ВВП соответственно: 0,0096 и 5,439 (для 1980 г.) и изменения в 1% сильно отличаются.

2. Проблема гетероскедастичности характерна для перекрестных данных и довольно редко встречается при рассмотрении временных рядов.