При наличии гетероскедастичности  и величина Ki может меняться от одного значения фактора к другому. При наличии гетороскедастичности вместо обычного МНК используют обобщенный МНК (взвешенный). Суть метода заключается в уменьшении вклада данных наблюдений, имеющих большую дисперсию в результате расчета.
и величина Ki может меняться от одного значения фактора к другому. При наличии гетороскедастичности вместо обычного МНК используют обобщенный МНК (взвешенный). Суть метода заключается в уменьшении вклада данных наблюдений, имеющих большую дисперсию в результате расчета.
1 случай. Если дисперсии возмущений известны 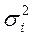 , то гетероскедастичность легко устраняется. Вводят новые переменные:
, то гетероскедастичность легко устраняется. Вводят новые переменные: 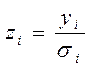 ;
; 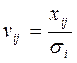 ;
; 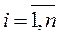 ,
, 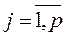 . Регрессионная модель в векторной форме
. Регрессионная модель в векторной форме
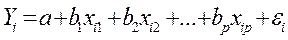 (*) /:
(*) /: 
 ,
, 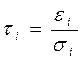 .
.
При этом 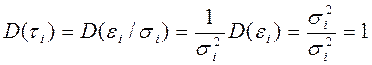 , т.е. модель гомоскедастична.
, т.е. модель гомоскедастична.
2 случай. Если дисперсии возмущений неизвестны, то делают реалистические предположения о значениях 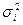 .
.
Например:
а) дисперсии 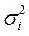 пропорциональны xi:
пропорциональны xi: 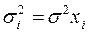 . Уравнение регрессии (*) делят
. Уравнение регрессии (*) делят
- на 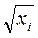 - в случае одной переменной; - на
- в случае одной переменной; - на 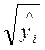 - в случае множественной регрессии.
- в случае множественной регрессии.
б) дисперсии 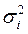 пропорциональны
пропорциональны 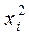 , т.е.
, т.е.
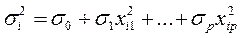 ,
,
Уравнение регрессии (*) делят на хi.
Пример. Воспользовавшись характером зависимости, полученным при использовании теста Глейзера
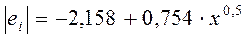 , разделим обе части уравнения на
, разделим обе части уравнения на 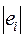
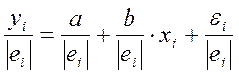 . Уравнение регрессии примет вид
. Уравнение регрессии примет вид
| ВЫВОД ИТОГОВ | ||||||||
| Регрессионная статистика | ||||||||
| Множественный R | 0,964 | |||||||
| R-квадрат | 0,929 | |||||||
| Нормированный R-квадрат | 0,927 | |||||||
| Стандартная ошибка | 5,502 | |||||||
| Наблюдения | ||||||||
| Дисперсионный анализ | ||||||||
| df | SS | MS | F | Значимость F | ||||
| Регрессия | 498,9 | 2E-23 | ||||||
| Остаток | 1150,5 | 30,28 | ||||||
| Итого | ||||||||
| Коэффициенты | Стандартная ошибка | t-статистика | P-Значение | Нижние 95% | Верхние 95% | |||
| Y-пересечение | -1,408 | 1,0935 | -1,288 | 0,206 | -3,622 | 0,806 | ||
| x/e | 0,337 | 0,0151 | 22,34 | 2E-23 | 0,3064 | 0,367 | ||
Получены новые оценки параметров линейного уравнения, в котором смягчена гетероскедастичность.
 2014-02-02
2014-02-02 1405
1405







