2014-02-02
635
Приложения производной функции
(Правило раскрытия неопределенносте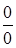й 
и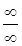 
).
Требуется вычислить предел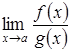 
, причем функции в числителе и знаменателе – дифференцируемы в окрестности точки 
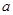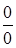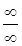и имеет место она из неопределенностей или , то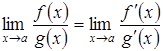 
.
Доказательство (для неопределенности 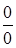). Поскольку 
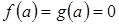, (иначе не будет указанной неопределенности), из теоремы Коши имеем
.
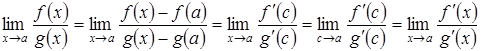Здесь использовалось, что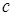 
находится между 
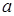и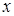 
, следовательно, пр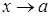и 
и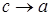 
.
Примеры.
1) 
.
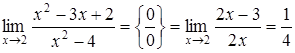Раньше это пример решался с помощьютождественного преобразования
.
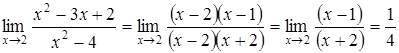2) 
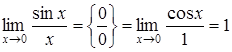(доказан первый замечательный предел).
