Следует отличать минимумы и максимумы функций от наибольшего и наименьшего ее значений на заданном отрезке. Функция может не иметь экстремумов в исследуемой области, а наименьшее и наибольшее в этой области значения она имеет всегда.
Чтобы определить наибольшее и наименьшее значения функции на заданном отрезке, необходимо подсчитать значения функции в точках экстремума, входящих в исследуемую область, а также в граничных ее точках и выбрать среди них наименьшее и наибольшее значения.
Пример.
Определить наибольшее и наименьшее значения функции 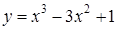 на отрезке
на отрезке 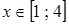 .
.
Находим точки, в которых производная обращается в нуль
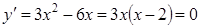 , получаем две точки, одна из которых
, получаем две точки, одна из которых 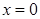 не входит в исследуемую область, добавляем к ним граничные точки, тогда
не входит в исследуемую область, добавляем к ним граничные точки, тогда 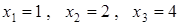 .
.
Определяем в этих точках значения функции 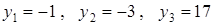 .
.
Таким образом, наименьшее в заданной области значение функции 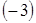 реализуется при
реализуется при 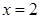 , наибольшее
, наибольшее 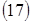 при
при 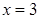 .
.
 2014-02-02
2014-02-02 496
496







