2014-02-02
282
Введем сеточные нормы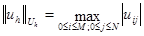 
; 
; 
.
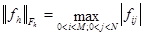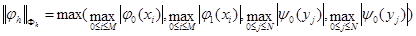Разностная схема (3), (4) называется устойчивой, если существуют такие положительные константы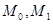 
, не зависящие от 
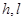, что для произвольной сеточной функции 
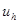выполняется неравенство 
.
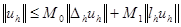Возьмем произвольную сеточную функцию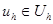 
, обозначим 
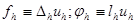и рассмотрим квадратный многочлен
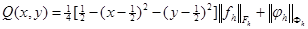. (5)
На множестве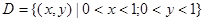 
выполняются неравенства
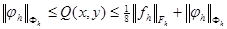. (6)
Применяя оператор Лапласа к многочлену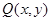 
, имеем 
.
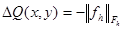Учитывая, что погрешность аппроксимации дифференциального оператора Лапласа разностным выражается через четвертые производные, получаем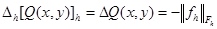 
.
Возьмем вспомогательную функцию 
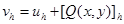. Применяя к ней разностный оператор Лапласа, получим 
.
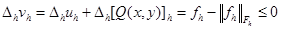В силу принципа максимума для разностного оператора Лапласа сеточная функция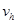 
принимает наименьшее свое значение на границе. На границе в соответствии с (6) имеем 
.
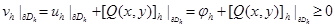Отсюда следует, что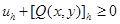 
или
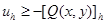. (7)
Используя вспомогательную функцию 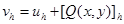, можно доказать, что
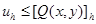. (8)
Объединяя (7) и (8), получаем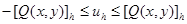 
или
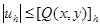. (9)
Из (9) и (6) следует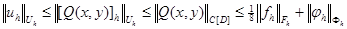 
. Устойчивость доказана.
Таким образом, разностная схема (3), (4) устойчива и аппроксимирует краевую задачу (1), (2) на ее решении. По доказанной ранее теореме решение 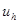разностной схемы будет сходиться к решению 
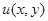краевой задачи.
При изложении материала за основу взяты страницы 530-531 учебного пособия: Бахвалов Н.С., Жидков Н.П., Кобельков Г.М.. Численные методы: Учеб. пособие для вузов.- М.:Наука. Гл. ред. физ.-мат. лит., 1987.
11.4. Метод матричной прогонки решения разностной схемы..
Задача Дирихле для уравнения Пуассона в единичном квадрате и ее разностная схема. Представление разностной схемы в матричном виде. Расчетные формулы метода матричной прогонки.
Использование алгебраических преобразований при выводе расчетных формул. Исследование метода матричной прогонки на устойчивость.
