Вывод расчетных формул метода матричной прогонки

Преобразование разностной схемы к матрично-векторному виду.

Перепишем уравнения (3) в виде

,

,

,

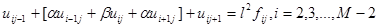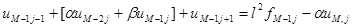где 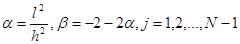. Обозначим векторы

;

.

.

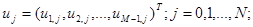
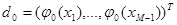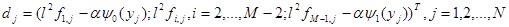Тогда разностную схему (3), (4) можно записать в матрично-векторной форме:

, (5a)

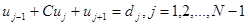, (5b)

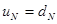, (5c)

где квадратная матрица C имеет вид

Равенство (5a) можно записать в ви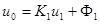де , где .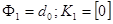

Пусть уже получено выражение

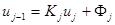. (6)

Подставляя (6) в (5b), получаем 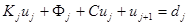или 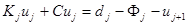. Откуда имеем 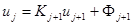, где

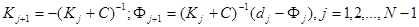. (7)

Расчеты по формуле (7) составляют прямой ход метода матричной прогонки, а по формуле (6) при 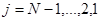- обратный ход.