Исследование метода матричной прогонки на устойчивость

Теорема. В расчетных формулах (7) матрицы 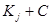имеют обратные.

Доказательство. Задано . Пусть 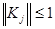. Будем использовать сферическую (евклидову) норму вектора и подчиненную ей матричную норму. Можно показать, что для данной симметричной матрицы 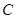все собственные значения удовлетворяют неравенству . Поэтому для произвольного вектора 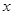справедливо .

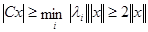Для произвольного вектора 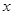имеем

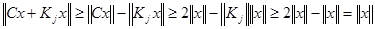. (8)

Отсюда получаем, что однородная система 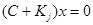имеет только тривиальное решение. Поэтому матрица 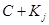системы неособенная и имеет обратную.

Возьмем произвольный вектор 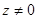. Для него существует ненулевой вектор 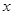, такой, что 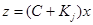. Из (8) следует 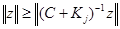или 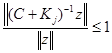Отсюда 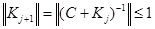. Теорема доказана.

При изложении материала за основу взяты

4) страницы 188-191 учебного пособия: Крылов В.И., Бобков В.В., Монастырный П.И. Вычислительные методы:, т.2.-М.:Наука. Гл. ред. физ.-мат. лит., 1977.

5) страницы 411-418 учебного пособия: Самарский А.А., Гулин А.В. Численные методы.- М.: Наука, 1989.

11.5. Разностные схемы для одномерного параболического уравнения.

Смешанная задача для одномерного параболического уравнения. Явная и неявная разностные схемы. Разрешимость неявной разностной схемы.

Оценка погрешности аппроксимации и исследование разностных схем на устойчивость.