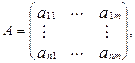
элементы которой aij являются вещественными числами. Пусть два лица, которых мы будем ниже называть первый игрок, второй игрок, играют в следующую игру. Первый игрок имеет n стратегий d1, ¼,d n и может выбрать любую по своему усмотрению; второй игрок имеет m стратегий q1, ¼,q m и тоже выбирает одну из них. При этом ни один из игроков не знает, какую стратегию выберет его противник. Если первый игрок выбрал стратегию d i, а второй игрок – стратегию q j, то потери первого игрока в этой ситуации равны числу aij. Таким образом, матрица A = (aij) является матрицей потерь первого игрока. Поскольку интересы игроков прямо противоположны, число aij можно называть также выигрышем второго игрока в результате ходов (d i, q j), а матрицу A – матрицей выигрышей второго игрока. Первый игрок действует так, чтобы уменьшить свои потери, второй игрок хочет увеличить свой выигрыш.
Введем следующие обозначения:
D = {d1, ¼, d n } – набор стратегий первого игрока,
Q = {q1, ¼, q m } – набор стратегий второго игрока.
Итак, простой A-игрой называется тройка объектов
{D, Q, A}
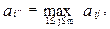 Обозначим
Обозначим
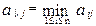 Видно, что ai есть максимальные потери, которые понесет первый игрок, если он будет следовать стратегии d i; a ¯ j – минимальные потери, которые он понесет, если второй игрок выберет стратегию q j.
Видно, что ai есть максимальные потери, которые понесет первый игрок, если он будет следовать стратегии d i; a ¯ j – минимальные потери, которые он понесет, если второй игрок выберет стратегию q j.
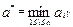 Определение 1. Число
Определение 1. Число
назовем верхней ценой игры.
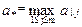 Определение 2. Число
Определение 2. Число
назовем нижней ценой игры.
Определение 3. Если a * = a *, то число
a = a * = a *
назовем ценой игры.
Лемма 1. Имеет место следующее неравенство:
a * ³ a *.
Доказательство. Для любых i, j справедливы неравенства
ai ³ aij ³ a ¯ j,
поэтому
ai ³ a ¯ j.
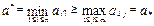 Стало быть
Стало быть
и лемма 1 доказана.
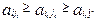 Определение 4. Будем говорить, что точка (i 0, j 0) является седловой (для матрицы A), если для всех i, j выполняются неравенства
Определение 4. Будем говорить, что точка (i 0, j 0) является седловой (для матрицы A), если для всех i, j выполняются неравенства
Цена игры существует тогда и только тогда, когда существует седловая точка.
Задачи к § 3
3.1. Первый игрок имеет $1000 для приобретения путевки на курорт. Предположим, что курс доллара к рублю составляет 1:31. Пусть по некоторым причинам покупка путевки переносится на месяц. В этой ситуации первый игрок должен ответить на вопрос: как поступить с деньгами? Опишите игру как простую А -игру, составьте матрицу потерь для первого игрока, найдите цену игры, если она есть.
3.2. Предприятие выпускает два вида продукции: мороженое (цена – 5 руб., себестоимость – 3 руб.) и пирожки (цена – 4 руб., себестоимость – 2,5 руб.). В холодную погоду продается 1000 штук мороженого и 6000 штук пирожков; в теплую погоду – 4000 штук мороженого и 1200 штук пирожков. Если продукцию не успели продать в день изготовления, то на следующий день ее продают по цене, в четыре раза меньшей, чем в день изготовления. Сформулируйте задачу как простую А -игру, составьте матрицу потерь для предприятия, найдите цену игры, если она существует.
3.3. Два противника сражаются на двух позициях. У первого противника – 4 полка, у второго – 3 полка. Каждый из противников может послать на позиции любое количество своих полков. Позиция считается выигрышной для участника, если он послал на нее большее количество полков, чем его оппонент, и выигрыш составляет «1+ число полков противника, плененных на этой позиции». В случае, когда количество полков на позиции совпадает, считаем, что на этой позиции ничья, и каждый игрок получает 0 очков. Общий выигрыш каждого участника равен сумме выигрышей на каждой позиции. Опишите игру как простую А -игру, составьте матрицу потерь для первого игрока, найдите цену игры, если она есть.
§ 4. Расширенная A – игра
Рассмотрим прямоугольную матрицу A размера n ´ m и отвечающую ей простую A –игру. Множества стратегий первого и второго игроков имеют вид
D = {d1, ¼, d n }, Q = {q1, ¼, q m }.
Назовем стратегии d i чистыми стратегиями первого игрока, а q j – чистыми стратегиями второго игрока.
Можно теперь расширить классы D, Q стратегий игроков, рассмотрев множества
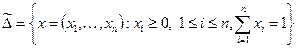
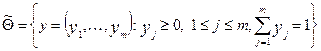
Вектор x = (x 1, ¼, xn) будем называть смешанной стратегией первого игрока, понимая под этим следующее: в соответствии с этой стратегией первый игрок с вероятностью xi выбирает чистую стратегию d i Î D. Аналогично интерпретируется смешанная стратегия y = (y 1, ¼, ym) для второго игрока.
Потери, которые понесет первый игрок, если он использует смешанную стратегию 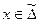 , а его оппонент смешанную стратегию
, а его оппонент смешанную стратегию 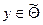 , имеют вид
, имеют вид

где T означает транспонирование матрицы-строки y = (y 1, ¼, ym), а запись xAyT понимается как произведение трех прямоугольных матриц в соответствии с обычными правилами умножения матриц.
Расширенной A–игрой мы будем называть тройку 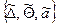 , где
, где 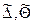 - классы смешанных стратегий первого и второго игроков соответственно, а ã = ã (x, y) – функция потерь первого игрока вида (1).
- классы смешанных стратегий первого и второго игроков соответственно, а ã = ã (x, y) – функция потерь первого игрока вида (1).
Обозначим
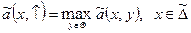
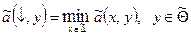
Видно, что ã (x,) – максимальные потери, которые понесет первый игрок, если он будет следовать стратегии x; ã (¯, y) –минимальные потери, которые он понесет, если второй игрок выберет стратегию y.
Определение 1. Число
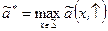
назовем верхней ценой расширенной A–игры.
Определение 2. Число
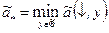
назовем нижней ценой расширенной A–игры.
Лемма 1. Имеет место следующее равенство
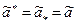
Стратегии 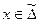 и
и 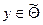 , удовлетворяющие равенству
, удовлетворяющие равенству 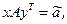 называются оптимальными стратегиями игроков, а (x, y, ã) – решением игры.
называются оптимальными стратегиями игроков, а (x, y, ã) – решением игры.
Лемма 2. Пусть число ã является ценой расширенной A–игры.
1) Для того, чтобы стратегия 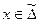 была оптимальной, необходимо и достаточно, чтобы для каждого j = 1,2,…,m выполнялось неравенство:
была оптимальной, необходимо и достаточно, чтобы для каждого j = 1,2,…,m выполнялось неравенство:
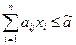
2) Для того, чтобы стратегия 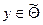 была оптимальной, необходимо и достаточно, чтобы для каждого i = 1,2,…,n выполнялось неравенство:
была оптимальной, необходимо и достаточно, чтобы для каждого i = 1,2,…,n выполнялось неравенство:
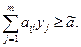
Суть леммы 2 состоит в том, что нахождение оптимальной стратегии сводится к решению системы неравенств и равенств:
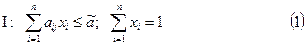
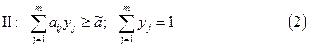
Лемма 3. Пусть число ã, стратегии x = (x1,¼, xn), y = (y1,¼, ym) удовлетворяют неравенствам (1), (2). Тогда они являются ценой игры и оптимальными стратегиями первого и второго игроков соответственно.
Если для некоторого индекса j в (1) выполняется строгое неравенство, т.е. 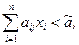 то соответствующий yj = 0.
то соответствующий yj = 0.
Если для некоторого индекса i в (2) выполняется строгое неравенство, т.е.
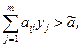 то соответствующий xi= 0.
то соответствующий xi= 0.
Доказательства этих лемм можно найти в [ ].
Задачи к § 4
4.1. Рассмотреть А-игру с матрицей потерь первого игрока:
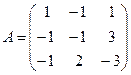
а) найти а*, а* и убедиться, что в простой А-игре нет цены;
б) составить систему линейных уравнений и неравенств для ã, x = (x1, x2, x3), y = (y1, y2, y3) в расширенной А-игре;
в) найти решение ã, x, y в расширенной А-игре.
4.2. Для матрицы
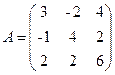
решить задачу 4.1.
 2014-02-02
2014-02-02 815
815








