Байесовский подход в теории игр

Предположим, что 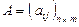- матрица потерь первого игрока. Предполагается, что известны вероятности, с которыми второй игрок применяет свои стратегии:

q_j = P (θ = θ_j), j=1,2,…, m,.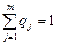

Для каждой стратегии δ_i считаются средние потери

.

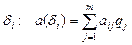Байесовской называется та стратегия, для которой средние потери минимальны:

δ*: а (δ*) =.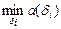

Пример 1. Пусть первый игрок имеет 10⁶ руб.; он может хранить их дома (стратегия δ ₁) либо поместить в банк под 10% годовых (стратегия δ ₂). Его противник (банк) имеет тоже две стратегии: θ ₁ – нормальная работа банка в течении года; θ ₂ – в течении года банк лопнет и вкладчик потеряет свои деньги. Матрица потерь первого игрока имеет вид:

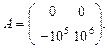
Поскольку а * = а _* = 0, то игра имеет цену а = 0 и оптимальная (чистая) стратегия первого игрока в этой А -игре существует. Это δ ₁, т.е. первый игрок, следующий минимаксной стратегии, должен хранить свои деньги дома.

Рассмотрим теперь байесовскую постановку данной задачи. Пусть априорное распределение имеет вид

q ₁ = P (θ = θ ₁) = 0,9999, q ₂ = P (θ = θ ₂) = 0,0001.

Иначе говоря, вероятность разорения банка в течении года равна 0,0001, т.е. достаточно мала. Тогда средние (байесовские) потери первого игрока равны соответственно

а (δ ₁) = 0 q ₁ + 0 q ₂ = 0, a (δ ₂) = q ₁(-10⁵) + q ₂10⁶ = -99890.

Поэтому байесовская стратегия в этой задаче равна δ ₂. Иначе говоря, банки разоряются очень редко (в странах с нормальной банковской системой), поэтому деньги хранить выгоднее в банке, чем дома.

Задачи к § 10

10.1. Рассмотрите игру с матрицей потерь первого игрока

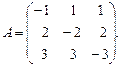
Найти: а) байесовскую стратегию первого игрока, если известно априорное распределение 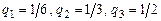стратегий второго игрока;

б) подобрать такое априорное распределение (q ₁, q ₂, q ₃), чтобы байесовская стратегия, отвечающая ему, имела вид (0,1,0).

10.2. Молодой бизнесмен М планирует посетить Объединенные Арабские Эмираты и с этой целью планирует занять в банке $5000. Если его дела пойдут успешно (стратегия θ ₁), он обещает через 3 месяца вернуть своему кредитору взятые деньги плюс 10%; в противном случае (стратегия θ ₂) он не сможет вернуть деньги.

У банка есть тоже две стратегии:

δ ₁ = {дать бизнесмену М деньги}; δ ₂ = {не дать бизнесмену М деньги}.

а) Найти минимаксную стратегию банка; б) допустим известны q _j, при каких значениях q₂ байесовской стратегией банка будет δ ₁.