Статистические игры

Эти игры иначе называются играми с экспериментом. Всегда ли выгодно проводить эксперимент? Если цена игры (допустим, потери) плюс затраты на эксперимент меньше цены игры без эксперимента, то в этом случае имеет смысл перейти к статистической игре.

Опишем статистическую игру на пример е. Предположим, что у нас имеется матрица потерь первого игрока.

Пусть δ₁, δ₂, δ₃ – чистые стратегии первого игрока, θ₁, θ₂ – чистые стратегии второго игрока. Найдем a^* = 3, a_* = 2, a^*≠ a_*. Проведем эксперимент, который имеет следующие исходы: t₁, t₂, t₃. Предположим, что известны вероятности P (t_i/θ_j):

	t1	t2	t3
θ1	0,6	0,25	0,15
θ2	0,2	0,3	0,5

Обозначим через S_ijk стратегию первого игрока. Она интерпретируется так: если исходом эксперимента является t₁, то первый игрок применит стратегию S_i, если t₂ – стратегию S_j, если t₃ – S_k; i, j, k =1, 2, 3.

Определенные таким образом стратегии будут чистыми стратегиями первого игрока в статистической игре. Всего таких стратегий будет 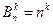, где n – число стратегий первого игрока, k – число исходов в эксперименте. В нашем случае таких исходов будет 3³=27.

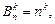Определим потери первого игрока: L(S_ijk, q₁), L(S_ijk, q₂).

Например,

L(S₂₃₁, q₁) = 0,6×1 + 0,25×3 + 0,15×0 = 1,35,

L(S₂₃₁, q₂) = 0,2×3 + 0,3×2 + 0,5×5 = 3,7.

Мы получаем в данном случае 27 пар таких значений и получаем игру порядка 27´2 с матрицей потерь, элементами которой и являются эти значения. Составление этой матрицы предлагается читателю (см.задачу 11.1)

Эту задачу можно решить обычными способами. Но мы перейдем к S-игре.

На плоскости отмечаем точки S_ijk(L(S_ijk, q₁), L(S_ijk, q₂)) (схематически – см.рис.1).

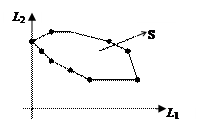Рис.1

Наряду с исходными, чистыми стратегиями рассматриваем смешанные стратегии первого игрока.

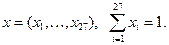
Класс всех смешанных стратегий S есть некоторое выпуклое множество:

Решение в этой игре выглядит так: x = (x₁, ¼, x₂₇). Для нахождения оптимальной стратегии можно применить два подхода: минимаксный и байесовский.

Минимаксный подход

Алгебраически: рассмотрим матрицу 27´2, затем процедурой доминирования приходим к матрице 7´2 и решаем задачу как игру n´2.

Графически: строим квадрат и увеличиваем стороны квадрата до касания с областью S (либо проводим биссектрису) и точка касания будет соответствовать минимаксному решению. Если первое касание происходит со стороной квадрата, то оптимальное решение находится среди чистых стратегий. Если первое касание происходит вершиной квадрата, то оптимальное решение находится среди смешанных стратегий. Если же сторона квадрата совпадает с ребром области S, то существуют альтернативные оптимальные решения.

В рассмотренном примере первое касание происходит с вершиной квадрата (рис.2). Точка касания S_M соответствует оптимальному решению.

Рис. 2

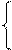Найдем точку S_M. Как известно, S_M = xS₂₃₃ + (1-x)S₃₃₃ или

L(S_M, q₁) = xL(S₂₃₃, q₁) + (1-x)L(S₃₃₃, q₁)

L(S_M, q₂) = xL(S₂₃₃, q₂) + (1-x)L(S₃₃₃, q₂)

Эта точка является вершиной квадрата и значит, что её координаты равны. Т.е. приравниваем правые части уравнений и получаем, что x= 5/7. Стратегия S_M выглядит следующим образом: с вероятностью 5/7 первый игрок применяет стратегию S₂₃₃, а с вероятностью 2/7 – стратегию S₃₃₃.

Итак, оптимальная стратегия первого игрока записывается так: x_M = (0,0,..., 0, 5/7, 0,..., 2/7).

Байесовский подход

Алгебраически: Пусть имеется априорная информация, т.е. известны вероятности q₁ = P (q =q₁) и q₂ = P (q =q₂), q₁ + q₂ =1. Найдём средние потери первого игрока при стратегии S: L_ср(S) = q₁L(S, q₁) + q₂L(S, q₂). Далее, среди них выберем минимальные, т.е S_d: minL_cp(S) = L_cp(S_d).

Графически: на плоскости строим прямую (линию уровня) q₁L₁ + q₂L₂ = d, взяв d произвольно. Затем двигаем эту линию произвольно до первого касания с S. Эта прямая будет либо касаться точкой, либо совпадать с ребром области S. Если это будет точка, то оптимальная стратегия находится среди чистых стратегий, если прямая совпадет с ребром области S, то это означает, что у первого игрока есть множество альтернативных оптимальных стратегий. Как видно, в этом подходе хотя бы одна чистая стратегия будет оптимальной.

Пусть в рассматриваемом примере q₁ = 1/3 и q₂ = 2/3. Построим прямую 1/3L₁ + 2/3L₂ = d. Возьмем d = 1/3. В этом случае точка касания будет в точке S₂₃₃. Найдем средние потери: L_cp(S₂₃₃) = 1/3×1,8 + 2/3×2,2 = 2,06.

Задачи к § 11

11.1. Привести полное решение примера, рассмотренного в § 11.

11.2. Когда мистер Смит вернулся домой, миссис Смит сообщила ему, что из коробки с бисквитами пропала дюжина бисквитов. Бисквиты мог съесть сын Джон или соседские дети, которые приходили днем в гости и были оставлены одни, когда миссис Смит на 10 минут отлучилась. Мистер Смит считает, что ели сын Джон виноват, то его следует наказать. Он составил следующую матрицу потерь:

Состояние природы	d1 (наказать)	d2 (не наказывать)
q1 (виновен) q2 (невиновен)

Супруги Смит решают взять за основу своих действий следующий эксперимент: они наблюдают за сыном во время ужина и замечают, как он ест – охотно (t₁), умеренно (t₂), плохо (t₃). Семейный врач предложил следующую оценку распределений вероятностей этих данных:

Состояние природы	t1	t2	t3
q1 q2	0,1 0,2	0,4 0,6	0,5 0,2

а) перечислить все чистые стратегии и найти для каждой отвечающие ей потери;

б) изобразить стратегии в виде точек на плоскости;

в) изобразить на плоскости класс всех смешанных стратегий и найти класс допустимых стратегий;

г) на основе чистых допустимых стратегий сформулировать расширенную А-игру;

Найти решение этой А-игры графически:

а) используя минимаксный подход;

б) используя байесовский подход при q₁ = 1/3 и q₂ = 2/3.