Гистограмма

Таблица 5.2

Данные о температуре запекания и доле дефектов

Температура, оС	Доля дефектов, %		Температура, оС	Доля дефектов, %
	0,4		0,3
	0,3		0,2
	0,4		0,1
	0,4		0,1
	0,4		0,1
	0,3		0,1
	0,3		0,1
	0,2		0,1
	0,2		0,2
	0,2		0,1
	0,4		0,1

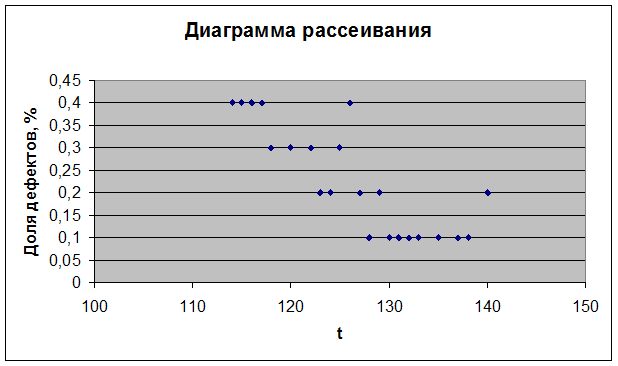
Рис. 5.3. Диаграмма рассеивания

для температуры запекания и доли дефектов

Учет фактора времени -

диаг­рамма рас­сеивания с временным лагом

В некоторых случаях, кроме набора пар значений исследуемых пе­ре­мен­ных (x₁, y₁), (x₂, y₂), …, (x_n, y_n), имеется также информация о периодических мо­ментах времени t₁, t₂, …, t_n, как показано в табл. 5.3. Тогда при проведении ана­лиза появляется возможность учесть фактор времени. Для этого строят диаграм­му рассеивания, смещая значения переменной y относительно фак­то­ра x: (x₁, y₂), (x₂, y₃), …, (x_n-1, y_n), (x_n, y_n+1)*. Полученный график называют диаг­раммой рас­сеивания с временным лагом (t₂ ‑ t₁). Временной лаг - это сдвиг по вре­мени меж­ду значениями переменных x и y. Аналогично могут быть по­строены диаграммы рассеивания с временным лагом (t₃ ‑ t₁), (t₄ ‑ t₁) и т.д. В не­которых слу­чаях переменные x и y лучше коррелируют между собой при на­личии того или иного временного лага. Целью подобного анализа яв­ля­ется оцен­ка ве­ли­чи­ны временного лага, при котором достигается наи­выс­шая кор­ре­ляция меж­ду показателем качества y и влияющим фактором x.

Таблица 5.3.

Набор данных с учетом фактора времени

Время	t1	t2	t3	…	tn-1	tn
x	x1	x2	x3	…	xn-1	xn
y	y1	y2	y3	…	yn-1	yn

Пример 6. Поставщиками компании-потребителя, занимаю­щей­ся сборкой из­де­лий, являются два завода, которые изготовляют од­но­типные детали двух мо­де­лей: 1 и 2. Введем обозначения: x - чис­ло рекламаций на деталь модели 1; y - число рекламаций на деталь мо­дели 2. Распределение числа рекламаций по ме­ся­цам пред­став­ле­но в табл. 5.4. С использованием про­грам­м (MS Excel, Statistica и т.п.) построить диаграмму рас­сеи­ва­ния, сде­лать вывод о наличии или отсутствии корреляции между чис­лом ре­кла­ма­ций по деталям моделей 1 и 2. Подтвердить сде­лан­ный вывод путем вы­чис­ле­ния коэффициента корреляции r.

Пример 7. Построить диаграммы рассеивания для данных табл. 5.4 с вре­мен­ным лагом 1, 2 и 3 месяца. Путем сравнения диаг­рамм определить, при каком вре­менном лаге достигается наи­выс­шая корреляция между числом рек­ла­ма­ций на детали моделей 1 и 2. Рас­считать коэффициенты корреляции для всех ди­аграмм рас­сеи­ва­ния. Проанализировать полученные результаты.

Таблица 5.4.

Исходные данные к примерам 6 и 7

Распределение числа рекламаций на детали моделей 1 (x) и 2 (y) по месяцам

Месяц

I

II

III

IV

V

VI

VII

VIII

IX

X

XI

XII

x

y

- это диаграмма столбцов, показывающая число точек, по­па­дающих в заданный интервал (класс, карман). Это число точек обычно называют частотой.

Кроме абсолютной частоты, при построении гис­тограмм иногда ис­поль­зуется относительная частота или частость. Ее по­лучают путем деления аб­солютной частоты на общее число обсле­до­ван­ных деталей (на­блюдений).

Три важных параметра гистограммы:

v центр;

v ширина;

v фор­ма.

Таблица 6.1.

Таблица частот

для распределения деталей по твердости HB покрытия

Номер ин­тервала	Интервал Изменения HB	Середина интервала	Частота	Частость
	350 < HB £ 360			0,00
	360 < HB £ 370			0,01
	370 < HB £ 380			0,05
	380 < HB £ 390			0,13
	390 < HB £ 400			0,24
	400 < HB £ 410			0,23
	410 < HB £ 420			0,16
	420 < HB £ 430			0,12
	430 < HB £ 440			0,04
	440 < HB £ 450			0,02
Итого:				1,00

Абсолютная частота, ед.

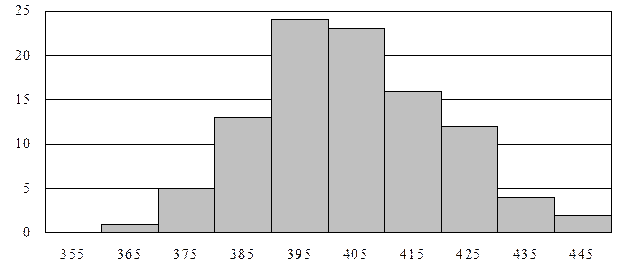
Твердость покрытия HB, кГ/мм²

Рис. 6.1. Гистограмма распределения деталей по твердости покрытия

Типичные формы гистограмм

а). Обычная (колоколообразная) гистограмма (рис. 6.2, а);

б). Гистограмма распределения с дву­мя пиками (рис. 6.2, б);

в). Гистограмма типа плато (рис. 6.2, в);

г). Гистограмма гребенчатого (мультимодального) типа (рис. 6.2, г);

д). Гистограмма положительно ско­шен­ного распределения (рис. 6.2, д);

е). Гистограмма усеченного слева распределения с поло­жи­тель­но ско­шенным "хвостом" (рис. 6.2, е);

ж). Гистограмма с изолированным пиком (рис. 6.2, ж);

з). Гистограмма с пиком на краю (рис. 6.2, з).

­
а) б)

в) г)

д) е)

ж) з)

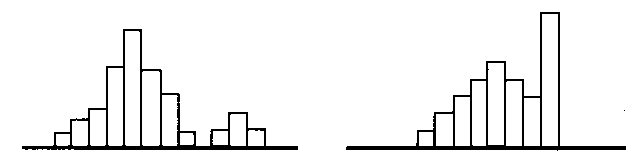
Рис. 6.2. Типичные структуры гистограмм