План
Примерный план лекции №6 и основные определения.
Контрольні запитання
Відповідність між різними адресами
Символьні адреси
Числові адреси є зручними для адміністрування, але для користувачів така адресація є незручною, тому для мереж різного масштабу існують символьні імена, які однозначно ідентифікують комп’ютер чи групу вузлів і зазвичай, мають змістовні назви – admin, student, decanat, site.ua.
Відповідністю між адресами різних типів займається служба розподілу адрес, яка може бути централізованою або розподіленою.
Для централізованого підходу в мережі виділяється один комп’ютер – сервер імен, в якому зберігається таблиця відповідності адрес різних типів (МАС, ІР, символьних). Решта комп’ютерів мережі звертаються до нього.
При розподіленому підході, кожний комп’ютер сам вирішує цю задачу. Перед початком передачі він відправляє до всіх вузлів широкомовне повідомлення, щоб відгукнувся власне вузол з заданою числовою адресою або символьним іменем. Запит отримують всі вузли, порівнюють вказану адресу зі своєю. Відгукується той вузол, де збіглася адреса і до нього скеровується повідомлення.
При розподіленому підході не потрібно виділяти сервер імен і задавати таблицю відповідності, але такі широкомовні повідомлення перевантажують мережу.
Централізований підхід застосовують у великих мережах, а розподілений – у невеликих.
1. Які вимоги висуваються до адресації вузлів та схеми її призначення?
2. Які функції покладено на широкомовні адреси?
3. Яка адреса є основною для отримання послуг локальної мережі?
4. Що позначає ІР-адреса комп’ютера?
5. Як розподіляються адреси за системою класів ІР-адрес?
6. Скільки байтів відведено для позначення номера мережі класу С?
7. Для чого введено автономні ІР-адреси?
8. Які дії покладено на ІР-адресу, перший октет якої є 127?
9. Як встановлюється відповідність між адресами різних типів?
10. Які функції покладено на сервер імен в локальних мережах?
Темы: Теория фирмы: описание и свойства технологий; краткосрочный и долгосрочный период; максимизация прибыли; минимизация издержек
- Описание технологии: производственная функция, изокванты, предельный продукт, предельная норма технологического замещения, отдача от масштаба.
- Примеры технологий.
- Максимизация прибыли в краткосрочном и долгосрочном периодах. Сравнительная статика.
- Минимизация издержек: задача, характеристика решения, графическая иллюстрация; слабая аксиома минимизации издержек.
Производственная функция 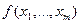 показывает максимальный объем выпуска
показывает максимальный объем выпуска 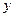 , который может быть получен из факторов производства
, который может быть получен из факторов производства 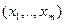 .
.
Изокванта – это линия уровня производственной функции 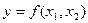 в пространстве факторов производства, т.е. это множество комбинаций факторов производства
в пространстве факторов производства, т.е. это множество комбинаций факторов производства 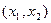 , позволяющих произвести в точности данный уровень выпуска
, позволяющих произвести в точности данный уровень выпуска 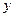 .
.
Если производственная функция дифференцируема, то предельным продуктом фактора производства 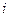 называется
называется 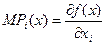 , т.е. предельный продукт показывает приращение выпуска, вызванное малом увеличением количества данного фактора производства.
, т.е. предельный продукт показывает приращение выпуска, вызванное малом увеличением количества данного фактора производства.
Предельная норма технологического замещения второго фактора производства первым (MRTS12) показывает, от какого объема второго фактора должна отказаться фирма, чтобы увеличив объем использования первого фактора на малую величину, произвести тот же уровень выпуска. Предельная норма технологического замещения характеризует наклон изокванты (по абсолютной величине) в пространстве факторов производства:  .
.
Отдача от масштаба:
Производственная функция 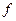 демонстрирует
демонстрирует
1. возрастающую отдачу от масштаба (IRTS), если для любого числа t>1
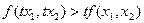
2. убывающую отдачу от масштаба (DRTS), если для любого числа t>1
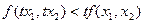
3. постоянную отдачу от масштаба (CRTS), если для любого положительного числа t 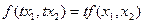 .
.
Задача максимизации прибыли:
1) Краткосрочный период (один из факторов производства фиксирован)
Пусть фирма производит выпуск 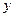 из двух факторов производства в соответствии с производственной функцией
из двух факторов производства в соответствии с производственной функцией 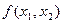 , и пусть количество фактора 2 фиксировано на уровне
, и пусть количество фактора 2 фиксировано на уровне 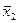 .
.
Тогда задача максимизации прибыли фирмы в краткосрочном периоде имеет вид:
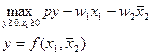
Характеристика внутреннего решения (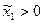 ):
): 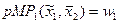 .
.
2) Долгосрочный период (все факторы производства переменны):
Тогда задача максимизации прибыли фирмы в долгосрочном периоде имеет вид:
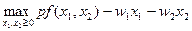 .
.
Характеристика внутреннего решения (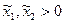 ):
): 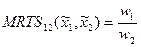 .
.
Решением задачи максимизации прибыли являются функции (безусловного) спроса на факторы производства: 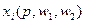 ,
, 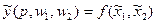 - это функция предложения фирмы, соответственно,
- это функция предложения фирмы, соответственно, 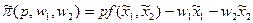 - функция прибыли фирмы.
- функция прибыли фирмы.
Слабая аксиома максимизации прибыли (Weak Axiom of Profit Maximization (WAPM)): Предположим, что при ценах 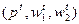 фирма, максимизируя свою прибыль, выбрала комбинацию факторов и выпуска
фирма, максимизируя свою прибыль, выбрала комбинацию факторов и выпуска 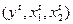 . А при ценах
. А при ценах 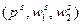 -
- 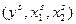 . Тогда должны выполняться следующие соотношения:
. Тогда должны выполняться следующие соотношения:
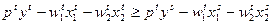 и
и 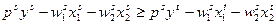 . Из слабой аксиома максимизации прибыли следует, что 1) выпуск фирмы не убывает с ростом цены готовой продукции; 2) спрос на фактор производства не возрастает по своей цене (т.е. в производстве отсутствует аналог товара Гиффена).
. Из слабой аксиома максимизации прибыли следует, что 1) выпуск фирмы не убывает с ростом цены готовой продукции; 2) спрос на фактор производства не возрастает по своей цене (т.е. в производстве отсутствует аналог товара Гиффена).
Задача минимизации издержек:
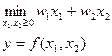
Решением этой задачи являются функции условного спроса на факторы производства 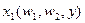 ,
, 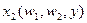 . Подставив функции условного спроса на факторы производства в целевую функцию задачи получим функцию издержек:
. Подставив функции условного спроса на факторы производства в целевую функцию задачи получим функцию издержек: 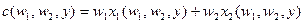 . Функция издержек показывает минимальные издержки производства
. Функция издержек показывает минимальные издержки производства 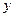 единиц выпуска при ценах факторов производства
единиц выпуска при ценах факторов производства 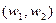 .
.
Слабая аксиома минимизации издержек (weak axiom of cost minimization WACM):
Пусть при ценах 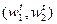 фирма, минимизируя издержки производства выпуска
фирма, минимизируя издержки производства выпуска 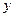 , выбрала комбинацию факторов
, выбрала комбинацию факторов 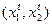 . А при ценах
. А при ценах 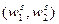 минимальные издержки производства того же объема выпуска
минимальные издержки производства того же объема выпуска 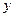 достигаются при комбинации факторов
достигаются при комбинации факторов 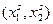 . Тогда должно быть выполнены следующие соотношения:
. Тогда должно быть выполнены следующие соотношения:
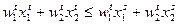 и
и 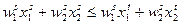 .
.
 2014-02-02
2014-02-02 377
377







