1) Определить длину исходной совокупности элементов  .
.
2) Определить длину искомой выборки 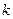 .
.
3) Выяснить, целесообразно ли искомую выборку разбивать на подвыборки, и каковы параметры этих подвыборок?
4) Выяснить, допускается ли в выборках (подвыборках) повторение элементов?
5) Выяснить, учитывается ли в выборке (подвыборке) порядок следования элементов?
6) Выяснить, как, зная число подвыборок, получить число искомых выборок (какое правило требуется использовать: сложения или умножения)?
7) Вычислить число подвыборок, а затем число искомых выборок.
Пример 1. Имеются 3 различные книги: А, В и С. Сколькими различными способами их можно расставить на полке?
Решение. Длина исходной совокупности элементов 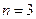 . Длина искомой выборки
. Длина искомой выборки 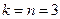 . Так как все книги различны, то повторение элементов не допускается. Так как книги требуется расставить на полке, то порядок следования элементов в выборке важен. Таким образом, искомые выборки представляют собой перестановки без повторений, тогда число искомых выборок
. Так как все книги различны, то повторение элементов не допускается. Так как книги требуется расставить на полке, то порядок следования элементов в выборке важен. Таким образом, искомые выборки представляют собой перестановки без повторений, тогда число искомых выборок 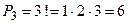 . Следовательно, существует 6 способов расстановки книг.
. Следовательно, существует 6 способов расстановки книг.
Пример 2. Из трех различных книг А, В и С две отбирают на выставку. Сколько выставочных комплектов можно составить?
Решение. Длина исходной совокупности элементов 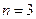 . Длина искомой выборки
. Длина искомой выборки 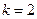 . Так как все книги различны, то повторение элементов не допускается. Так как книги требуется отобрать на выставку, то важно, какие книги будут выбраны и неважно, в каком порядке отбирать книги, то есть порядок следования элементов в выборке неважен. Таким образом, искомые выборки представляют собой сочетания без повторений, тогда число искомых выборок
. Так как все книги различны, то повторение элементов не допускается. Так как книги требуется отобрать на выставку, то важно, какие книги будут выбраны и неважно, в каком порядке отбирать книги, то есть порядок следования элементов в выборке неважен. Таким образом, искомые выборки представляют собой сочетания без повторений, тогда число искомых выборок 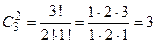 . Следовательно, можно составить 3 выставочных комплекта.
. Следовательно, можно составить 3 выставочных комплекта.
Пример 3. Имеется 5 карточек с буквами A, B, C, D, E. Сколько различных «слов», содержащих не более трех букв, можно из них составить?
Решение. Длина исходной совокупности элементов 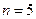 . По условию задачи каждое «слово» содержит либо 1, либо 2, либо 3 буквы, то есть имеется 3 искомых подвыборки, длины которых
. По условию задачи каждое «слово» содержит либо 1, либо 2, либо 3 буквы, то есть имеется 3 искомых подвыборки, длины которых 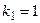 ,
, 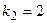 и
и 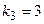 . Так как все карточки различны, то повторение элементов в каждой подвыборке не допускается. Так как «слова» отличаются не только составом букв, но и порядком следования элементов, то в каждой подвыборке порядок следования элементов учитывается. Таким образом, искомые подвыборки представляют собой размещения без повторений. Вычислим число искомых подвыборок.
. Так как все карточки различны, то повторение элементов в каждой подвыборке не допускается. Так как «слова» отличаются не только составом букв, но и порядком следования элементов, то в каждой подвыборке порядок следования элементов учитывается. Таким образом, искомые подвыборки представляют собой размещения без повторений. Вычислим число искомых подвыборок.
При 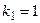
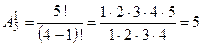 «слов».
«слов».
При 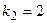
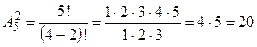 «слов».
«слов».
При 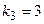
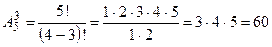 «слов».
«слов».
Так как «слово», составленное только из одной буквы не может содержать только две или только три буквы; «слово», составленное только из двух букв не может содержать только одну или только три буквы; «слово», составленное только из трех букв не может содержать только одну или только две буквы, то действия по составлению «слов» только из одной, только из двух и только из трех букв попарно несовместны. Поэтому для подсчета общего числа искомых выборок применяем правило сложения. Тогда число «слов», содержащих не более трех букв 5+20+60=85.
 2014-02-02
2014-02-02 2618
2618








