Определение поля событий

Поле событий

Замечание. Рассуждения настоящего параграфа относятся не только к классическому определению вероятности, но и ко всем дальнейшим обобщениям.

Будем считать фиксированным комплекс условий 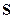и рассмотрим некоторую систему событий 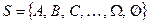, каждое из которых должно при каждом осуществлении комплекса 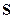произойти или не произойти. Между событиями системы 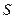могут существовать некоторые отношения, которые требуют определения и изучения.

Определение 1. Если при каждом осуществлении комплекса условий 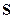, при котором происходит событие 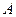, происходит и событие В, то будем говорить, что А влечёт за собой В (А является частным случаем В). Обозначается 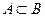или .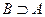

Определение 2. Если А влечёт за собой В и в то же время В влечёт за собой А, т.е. если при каждой реализации комплекса условий 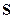события А и В оба наступают или не наступают, то будем говорить, что события А и В равносильны между собой. Обозначается .

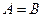Определение 3. Событие, состоящее в одновременном наступлении событий А и В, называется произведением(совмещением) событий А и В. Обозначается АВ.

Определение 4. Событие, состоящее в наступлении хотя бы одного из двух событий А и В, называется суммой событий А и В. Обозначается А+В.

Замечание. Определения суммы и произведения событий можно обобщить на любое конечное число событий.

Определение 5. Событие, состоящее в том, что событие А происходит, а событие В не происходит, будем называть разностью событий А и В. Обозначается .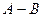

Пример. Игральная кость бросается один раз. События А – выпадение на верхней грани 6 очков, В – выпадение трёх очков, С – выпадение чётного числа очков, 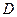- выпадение числа очков, кратного трём. Тогда события А, В, С и D связаны соотношениями: , , , , .

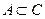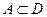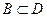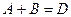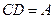Замечание. При всякой реализации комплекса условий S все достоверные события равносильны между собой. Будем обозначать их 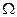. Все невозможные события также равносильны между собой. Будем обозначать их .

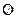Определение 6. Событие, заключающееся в том, что событие А не происходит, называется противоположным для А. Обозначается .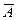

Замечание 1. Для противоположных событий одновременно выполняются соотношения: 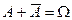, 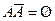(по определению).

Замечание 2. Для несовместных событий А и В справедливо соотношение .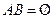

Определение 7. Если 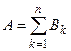и события попарно несовместны (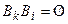при 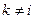), то говорят, что событие А подразделяется на частные случаи , , …,.

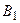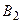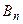Пример. Игральная кость, четное число очков.

Замечание. Во всех рассуждениях теории вероятностей равносильные события могут заменять друг друга. Поэтому условимся равносильные события считать тождественными.

Определение 8. Пусть имеется комплекс условий S и система событий S, наступающих или не наступающий после каждой реализации комплекса условий S. Полем событий называется такая система событий S, которая удовлетворяет следующим допущениям:

1) если системе S принадлежат события А и В, то ей принадлежат также события АВ, А+В, А-В;

2) система S содержит достоверное и невозможное события.

Замечание. Операции над событиями в поле событий обладают свойствами теоретико-множественных операций. Поэтому поле событий также называют алгеброй событий.