2014-02-02
7540
Классическое определение вероятности
Первичными понятиями теории вероятностей являются понятия опыта, события, вероятности, равновозможности (равновероятности).
Определение 1. Опытом (испытанием) будем называть всякое действие, которое может быть осуществлено неограниченное число раз в неизменных условиях (говорят «при всякой реализации определённого комплекса условий S»).
Определение 2. Событием (исходом) будем называть результат опыта (испытания).
Определение 3. Достоверным называется событие, которое обязательно произойдёт при всякой реализации данного опыта (при всякой реализации комплекса условий S).
Определение 4. Невозможным называется событие, которое заведомо не произойдёт при любой реализации данного опыта (при всякой реализации комплекса условий S).
Определение 5. Случайным называется событие, которое при реализации данного опыта (при всякой реализации комплекса условий S) может либо произойти, либо не произойти.
События обозначаются большими латинскими буквами: А, В, С и т. д.
Пример 1. Игральная кость. Монета. Монеты.
Замечание. Каждое из случайных событий обладает некоторой степенью возможности. Чтобы количественно сравнивать между собой события по степени их возможности нужно связать с каждым событием число, которое тем больше, чем более возможно событие.
Определение 6. Вероятностью события будем называть численную меру степени объективной возможности этого события.
Определение 7. События А и В будем называть равновозможными (равновероятными), если есть основания считать, что ни одно из этих событий не является более возможным, чем другие.
Пример 2. Симметричная игральная кость.
Определение 8. События называют несовместными, если появление одного из них исключает появление других событий в одном и том же испытании. В противном случае события называют совместными.
Определение 9. Совокупность событий Н1, Н2, …, Нn называется полной группой событий, если появление хотя бы одного события из совокупности Н1, Н2, …, Нn в одном испытании является достоверным событием.
Определение 10. Пространством элементарных событий (исходов) (группой случаев) будем называть полную группу попарно несовместных равновозможных случайных событий Н1, Н2, …, Нn. Каждое из событий Н1, Н2, …, Нn будем называть элементарным событием или элементарным исходом.
Пример 3. 2 монеты, пространство элементарных событий.
Замечание. Понятие пространства элементарных событий как полной группы попарно несовместных равновозможных случайных событий иногда называют классической схемой. Классическая схема возникла из азартных игр и явилась первоначальным этапом развития теории вероятностей. Возможны и неклассические схемы (например, схема Бернулли). В них под пространством элементарных событий понимают полную группу попарно несовместных событий, исключая равновозможность элементарных исходов.
Замечание. Часто возникают задачи, в которых требуется изучить возможность наступления не элементарного события, а одного из нескольких определённых элементарных событий.
Пример 4. Игральная кость. Выпадения числа очков, больше 3-х.
Определение 11. Если в задачеинтересует появление какого-то из определённых элементарных событий Нi1, Нi2, …, Нim, то будем говорить, что интересует наступление события А, состоящего в выпадении одного из m элементарных исходов Нi1, Нi2, …, Нim. Исходы Нi1, Нi2, …, Нim будем называть исходами,благоприятными появлению события А.
Определение 12 (классическое определение вероятности). Вероятностью события А называют отношение числа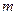 
элементарных исходов, благоприятных появлению события А к числу 
всех равновозможных несовместных элементарных исходов, образующих полную группу: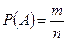 
. (2.1)
Свойство 1. Вероятность достоверного события равна единице.
Действительно, если событие достоверно, то каждый элементарный исход испытания благоприятствует событию. В этом случае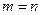 
и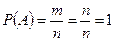 
.
Свойство 2. Вероятность невозможного события равна нулю.
Действительно, если событие невозможно, то ни один из элементарных исходов испытания не благоприятствует событию. В этом случае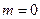 
и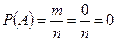 
.
Свойство 3. Вероятность случайного события есть положительное число, заключенное между нулем и единицей.
Действительно, случайному событию благоприятствует лишь часть из общего числа элементарных исходов испытания. В этом случае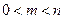 
, значит, 
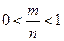, следовательно, 
.
Вывод. Вероятность любого события удовлетворяет неравенствам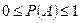 
.
Определение 12. Два несовместных события, образующих полную группу, называются противоположными.
Событие, противоположное событию А, обозначается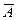 
.
Замечание. Формула (2.1) не является исчерпывающим определением вероятности. В общем случае она пригодна тогда и только тогда, когда опыт сводится к классической схеме случаев.
