2014-02-02
348
Нам необходимо найти минимум некоторой функции f (одной переменной) на интервале [a,b]. Будем считать, что f на данном интервале имеет ровно один минимум.
Простейший метод нахождения точки минимума – метод сечений:
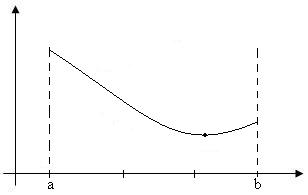Разобьем участок [a,b] на n интервалов и
рассмотрим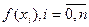 
. Предположим
минимум достигается при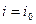 
, тогда
новый участок поиска будет [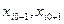
]
его снова разбиваем на новые участки
(критерий как в МПД, т.е.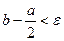 
).
Рассмотрим вариант n=3 (ежу понятно,
что делить меньше чем на 3 интервала
бессмысленно).
() (*)
На самом же деле выгоднее делить интервал не таким образом, а по методу золотого сечения.
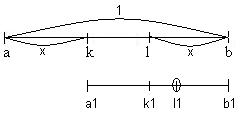
Пропорции деления (они сохраняются) были подобраны таким образом, что при переходе к новому интервалу нам необходимо вычислять значения f не в 2х новых точках, а в 1-ой, хотя при этом интервал поиска сокращается не в два раза (как было на предложенной схеме (*)), а чуть меньше, следовательно, этот вариант оказывается выгоднее, т.к. для достижения заданной точности нам придётся меньше раз вычислять значение f. 4 точки на первом шаге и по 1-ой новой точке на каждом последующем шаге, а не в 2х.
|
|
|
Найдём пропорции золотого сечения:
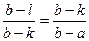
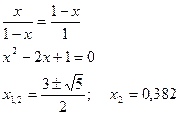
Итак, в алгебре метода золотого сечения заложены пропорции: 0,382; 0,236; 0,382.
Тема 9: Метод Монте-Карло.
