Свойства функции распределения вероятностей

Свойство 1. Для любых 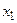и 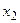из неравенства 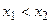следует, что .

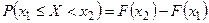Доказательство. Пусть А – событие, состоящее в том, что примет значение, меньшее 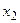, В – событие, состоящее в том, что примет значение, меньшее 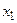, С – событие, состоящее в том, что 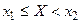. Тогда имеет место равенство 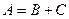. Так как события В и С несовместны, то .

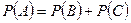Так как 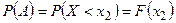, , 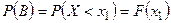, 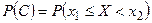то 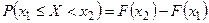, что и требовалось доказать.

Свойство 2. Для любых 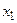и 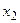из неравенства 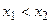следует, что 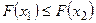, т.е. функция распределения любой случайной величины является неубывающей функцией.

Доказательство. Так как вероятность есть неотрицательное число, то (в силу свойства 1) 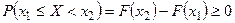и, следовательно, .

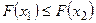Свойство 3. Для любого 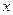справедливо неравенство .

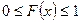Доказательство. Так как (по определению) 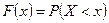, то по свойствам вероятности .

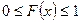Определение 8. Будем говорить, что функция распределения имеет при 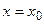скачок, если .

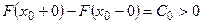Свойство 4. Функция распределения может иметь не более, чем счётное множество скачков.

Доказательство. Скачков размера, большего ½, может иметь не более одного; скачков размера от ¼ до ½ (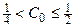) – не более трёх. Вообще, скачков размером от 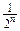до 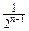может быть не более, чем 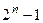. Все скачки можно пронумеровать, расположив их по величине, начиная с больших значений и повторяя равные значения столько раз, сколько скачков этой величины имеет функция . Пронумерованное множество счётно.

Определение 9. , .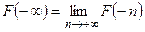

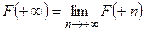Свойство 5. , .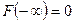

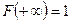Доказательство. Так как неравенство 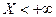достоверно, то 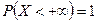. Обозначим 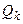событие, состоящее в том, что 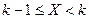. Так как событие 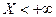эквивалентно сумме событий 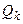, то на основании расширенной аксиомы сложения 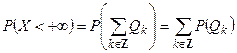. Следовательно, при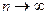

.

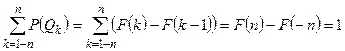Принимая во внимание неравенство 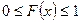, получаем, что , .

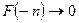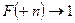Свойство 6. Функция распределения непрерывна слева.

Доказательство. Выберем какую-нибудь возрастающую последовательность 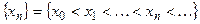, сходящуюся к 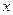. Обозначим 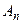событие 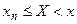. Тогда если 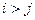, то 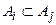и произведение всех событий 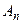есть невозможное событие. По аксиоме непрерывности должно быть

,

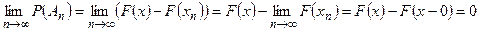Что и требовалось доказать.

Следствие. 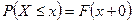. Доказывается аналогично.

Вывод. Каждая функция распределения является неубывающей, непрерывной слева и удовлетворяющей условию 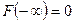, 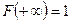функцией. Верно и обратное: каждая функция, удовлетворяющая перечисленным условиям, может рассматриваться, как функция распределения некоторой случайной величины.