Обычные (невероятностные) методы ЧИ хорошо работают только лишь при интегрировании функций небольшого количества переменных. При росте количества переменных, число узлов интегрирования стремительно растёт (экспоненциально).
Например, пусть необходимо найти интеграл 10-ти переменных с шагом h=0,1 по каждому измерению:
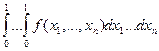 итого
итого 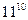 измерений – в подобном случае применяют метод Монте-Карло.
измерений – в подобном случае применяют метод Монте-Карло.
Рассмотрим первый вариант метода Монте-Карло:
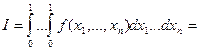 {среднему значению на кубе
{среднему значению на кубе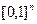 , как известно из мат. анализа среднее значение функции равно
, как известно из мат. анализа среднее значение функции равно 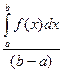 , следовательно, для функций многих переменных
, следовательно, для функций многих переменных 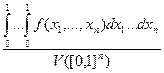 }.
}.
В то же время, как известно из теории вероятности, среднее эмпирическое значение при увеличении количества испытаний стремится к точному значению.
В нашем случае эмпирическое среднее (для N испытаний)
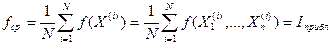 , таким образом, для нахождения
, таким образом, для нахождения 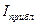 мы N раз находим значение функции f в N точках
мы N раз находим значение функции f в N точках  , каждая из которых имеет n координат, при этом, каждая координата – случайное число на отрезке [0,1]. Итак, random нам потребуется вызвать n*N раз.
, каждая из которых имеет n координат, при этом, каждая координата – случайное число на отрезке [0,1]. Итак, random нам потребуется вызвать n*N раз.
При каждом запуске метода Монте-Карло мы будем получать новые значения 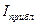 , но все они
, но все они 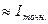
П.2. Второй вариант метода Монте-Карло (интегрирование не по n-мерному кубу, а по некоторой произвольной n-мерной области D).
Необходимо найти:



где П – прямоугольный параллелепипед ограничивающий область D.
П=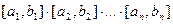
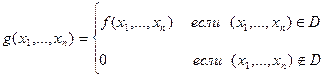
=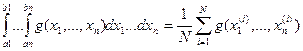
Чтобы получить равномерное распределение на 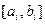 , берем random*
, берем random*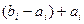 - все остальные вычисления аналогичны случаю n-мерного куба.
- все остальные вычисления аналогичны случаю n-мерного куба.
Недостатки:
Основная проблема, что в предложенном выше методе мы не можем достоверно оценить вероятность отклонения 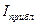 от
от 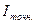 , мы знаем только лишь, что M(
, мы знаем только лишь, что M(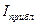 )=
)=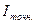 , т.е. при бесконечном количестве испытаний
, т.е. при бесконечном количестве испытаний 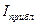 =
=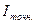 . А оценить разброс
. А оценить разброс 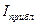 от
от 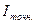 мы не можем, т.к. не знаем дисперсию.
мы не можем, т.к. не знаем дисперсию.
Оценить вероятность отклонения случайной величины от её мат. ожидания, можно с помощью неравенства Чебышева 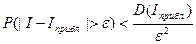 (9.1)
(9.1)
С ростом числа испытаний N, 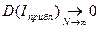 , а именно, если мы проведём N испытаний, то
, а именно, если мы проведём N испытаний, то 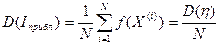 (9.2)
(9.2)
Если в (9.1) подставить формулу (9.2), то получим 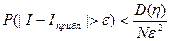
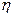 -не зависит от N и
-не зависит от N и 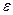 , зависит от g и области интегрирования D.
, зависит от g и области интегрирования D.
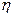 можно оценить, используя различные способы, например, найти эмпирическое значение дисперсии.
можно оценить, используя различные способы, например, найти эмпирическое значение дисперсии.
 2014-02-02
2014-02-02 404
404








