Полигон и функция распределения

Числовые характеристики дискретных случайных величин

Дискретные случайные величины их числовые характеристики и законы распределения

Замечание. Дискретные случайные величины могут принимать только конечное или счётное множество значений. Эти значения будем называть возможными значениями дискретной случайной величины .

Определение 1. Закон распределения дискретной случайной величины называется рядом распределения:

				…		…
				…		…

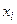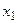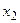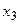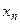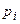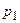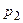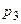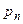При этом 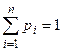, где суммирование распространяется на все (конечное или бесконечное) множество возможных значений данной случайной величины Х.

Определение 4. В прямоугольной системе координат 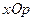отметим точки 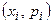и соединим их последовательно ломаными отрезками. Полученная ломаная называется многоугольником (полигоном) распределения случайной величины Х.

Замечание 1. Функция распределения вероятностей дискретной случайной величины задаётся равенством 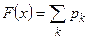, в котором суммирование распространяется на все те индексы, при которых 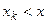. Функция распределения любой дискретной случайной величины разрывна, возрастает скачками при тех значениях 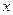, которые являются возможными значениями . Величина скачков функции в точке 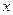равна разности 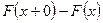. Если два возможных значения Х разделены интервалом, в котором других возможных значений Х нет, то на этом интервале функция распределения постоянна. Если возможных значений Х конечное число, например n, то функция распределения представляет собой ступенчатую кривую с 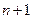интервалом постоянства. Если же возможных значений Х имеется счётное множество, которое может быть всюду плотным, так что интервалов постоянства у функции распределения дискретной случайной величины может и не быть.