Функциональная схема САР с ЦВМ в контуре управления
показана на рис.17.
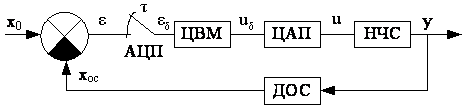
Рис.17.Функциональная схема САР с ЦВМ:
АЦП – аналого-цифровой преобразователь);
ЦАП – цифро-аналоговый преобразователь;
НЧС – непрерывная часть системы.
Диаграммы сигналов в контуре управления показаны на рис.18.
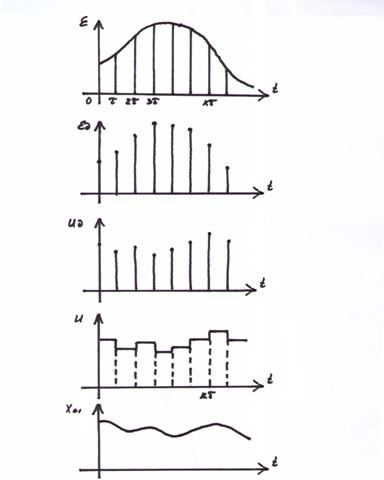 Рис.18. Диаграммы сигналов в контуре управления.
Рис.18. Диаграммы сигналов в контуре управления.
В контуре имеются 2 вида сигналов:
· дискретные сигналы 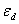 и
и 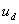 ,
,
· аналоговые сигналы x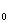 , ε, x
, ε, x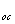 .
.
Дискретный сигнал f можно задать двумя способами:
можно задать двумя способами:
· бесконечной числовой последовательностью
f =(f
=(f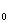 , f
, f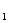 , ….,f
, ….,f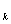 ,…), где f
,…), где f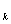 =f(kτ), последовательность f
=f(kτ), последовательность f называется решетчатой функцией.
называется решетчатой функцией.
· Z–изображением решетчатой функции.
Понятие о Z-преобразовании.
Z-изображением решетчатой функции f
называется сумма ряда:
f0 + f1z-1 + f2z-2 + …+ fkz-k + …=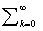 fkz-k = Z { f
fkz-k = Z { f }. (18) Иногда Z-изображение решетчатой функции f
}. (18) Иногда Z-изображение решетчатой функции f удобнообозначить символом F
удобнообозначить символом F (z).
(z).
Основные свойства Z-изображений:
1) сумме решетчатых функций соответствует сумма их Z-изображений:
Z{f + φ
+ φ } = Z{f
} = Z{f } + Z{φ
} + Z{φ };
};
2) постоянный множитель можно выносить за знак Z-изображения;
3) теорема запаздывания: если f 
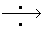 Z{ f
Z{ f  } и функция φ
} и функция φ запаздывает на n шагов, то φ
запаздывает на n шагов, то φ 
 z-nZ{ f
z-nZ{ f  },
},
например, при n=3:
φ ={0,0,0,f0,f1,f2, …}
={0,0,0,f0,f1,f2, …}  Z{φ
Z{φ } = 0 + 0z-1+0z-2+ f0z-3 + …=
} = 0 + 0z-1+0z-2+ f0z-3 + …=
z-3 (f0 + f1z-1 + …)= z-3 Z{ f }.
}.
В таблице 1 приведены Z-изображения решетчатых функций, полученных дискретизацией соответствующих непрерывных сигналов.
Для решетчатой функции f =(f
=(f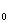 , f
, f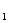 , ….,f
, ….,f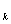 ,…), где f
,…), где f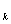 =f(kτ), вводится также понятие дискретного изображения по Лапласу в виде суммы ряда:
=f(kτ), вводится также понятие дискретного изображения по Лапласу в виде суммы ряда:
f0 + f1e-τp + f2e-2τp + … + fke-kτp + … = 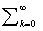 fke-kτp = D { f
fke-kτp = D { f }. (19)
}. (19)
Сравнивая выражение (19) с выражением для z-изображения решетчатой функции f (18), получим, что дискретное изображение по Лапласу:
(18), получим, что дискретное изображение по Лапласу:
D{ f } = D{f(kτ)} = F
} = D{f(kτ)} = F (z) | z = eτp (20).
(z) | z = eτp (20).
Таким образом, дискретное изображение Лапласа решетчатой функции f получается из Z-изображения Z{ f
получается из Z-изображения Z{ f  } заменой аргумента z на eτp.
} заменой аргумента z на eτp.
 2014-02-02
2014-02-02 520
520








