Сонаправленных и взаимно перпендикулярных колебаний. В некоторых случаях гармонические колебания удобно изображать при помощи метода векторных диаграмм

Метод векторных диаграмм. Сложение гармонических

В некоторых случаях гармонические колебания удобно изображать при помощи метода векторных диаграмм. Возьмём ось X и на ней точку О. Из этой точки отложим вектор длиной А под углом j к оси X (рис. 4.2). Если вращать этот вектор с частотой w, то проекция этого вектора на ось X будет изменяться по закону

x=Acos(wt+j).

Таким образом, проекция вектора на ось X будет совершать гармоническое колебание с круговой частотой, равной угловой скорости вращения вектора и с начальной фазой, равной углу, который образует вектор А с осью X в начальный момент времени.

Воспользуемся методом векторных диаграмм для сложения двух колебаний одинаково направленных и с одинаковой частотой. Т.е., пусть результирующее смещение будет суммой двух смещений x=x₁+x₂, причём

x₁=A₁cos(wt+j₁), x₂=A₂cos(wt+j₂)

Представим оба колебания при помощи метода векторных диаграмм (рис. 4.3). В соответствии с правилом сложения векторов получим результирующий вектор А. Из рисунка видно, что его проекция на ось Х равна сумме проекций слагаемых векторов х₁ и х₂. Другими словами, вектор А действительно является суммой двух колебаний. Этот вектор вращается с той же угловой скоростью, что и вектора-слагаемые, т.е.

x=Acos(w t+j), (4.8),

причём, как это видно из рис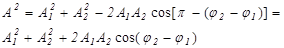. 4.9,

(4.9)

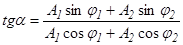. (4.10)

Мы продемонстрировали возможности метода векторных амплитуд на примере сложения двух колебаний. Особенно удобен этот метод, когда надо складывать много колебаний – мы просто складываем векторы по правилу сложения векторов.

Как следует из выражения (4.9), если разность фаз складываемых колебаний равна 0, то результирующая амплитуда будет просто равна сумме амплитуд. Складываемые колебания в этом случае называются синфазными, а колебания, у которых разность фаз не изменяется с течением времени, называются когерентными. Если же разность фаз равна p, то результирующая амплитуда будет равна разности амплитуд складываемых колебаний. О таких колебаниях говорят, что они происходят в противофазе. Если же частоты складываемых колебаний неодинаковы, то векторы-слагаемые будут вращаться с разными угловыми скоростями, а результирующий вектор будет изменяться по величине и вращаться с изменяющейся угловой скоростью. Результирующее колебание при этом уже не будет гармоническим.

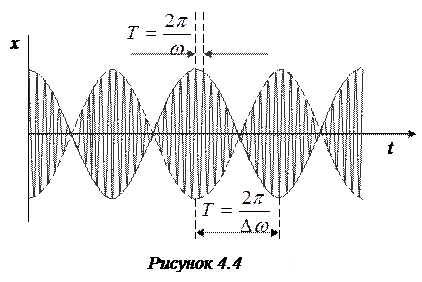
Особый интерес представляет сложение двух гармонических колебаний с близкими (но разными!) частотами. В этом случае результирующее колебание можно рассматривать как гармоническое с пульсирующей амплитудой. Такое колебание называют биениями.

Итак, будем складывать 2 колебания с близкими частотами, т.е. будем считать, что Dw = w₂-w₁ << w₂. Для упрощения формул будем складывать колебания с одинаковыми амплитудами, а начальные фазы обоих колебаний положим равными нулю:

x₁=Acoswt; x₂=Acos(w+Dw)t.

Применяя формулу сложения косинусов 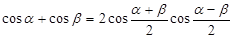, получим

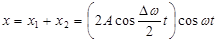. (4.11)

Здесь мы пренебрегли во втором сомножителе слагаемым 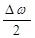по сравнению с w. График результирующей функции (4.17) показан на рис. 4.4. Из рисунка видно, что мы можем рассматривать результирующее колебание как гармоническое с периодически изменяющейся амплитудой:

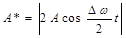. (4.12)

Пусть теперь частица одновременно совершает колебания в двух взаимно перпендикулярных направлениях, например, вдоль осей y и x. Фазу колебания вдоль оси х положим равной 0.

x=Acoswt; y=Bcos(wt+j). (4.13)

Чтобы получить уравнение траектории в координатах х и y, из уравнений (4.13) необходимо исключить время. Из первого уравнения (4.13) следует, что

. (4.14)

Теперь раскроем косинус во втором уравнении (4.13) в соответствии с формулой 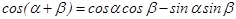. В результате получим

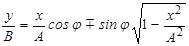. (4.14)

Возведём в квадрат выражение (4.14), приведём подобные члены и, последовательно, получим:

,

,

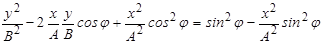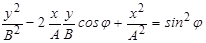. (4.15)

Последнее уравнение (4.15) представляет собой уравнение эллипса, оси которого повернуты произвольным образом относительно осей х и y. Ориентация осей и форма эллипса зависят от разности фаз j. Проанализируем выражение (4.15) для некоторых частных случаев.

1 Разность фаз складываемых колебаний: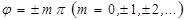. Тогда в выражении (4.86) cos j=±1; и sinj=0 и в результате вместо выражения (4.15) получим уравнение прямой (говорят, что эллипс вырождается в прямую):

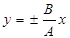(4.16)

Рисунок 4.5

где знак “+” соответствует нулю и чётным значениям m (рис. 4.5, а), а знак “–” соответствует нечётным значениям m (рис. 4.5, б). Результирующее колебание будет гармоническим с частотой ω и амплитудой . Угол . Такие колебания называются линейно-поляризованными.

2 Пусть теперь разность фаз складываемых колебаний: 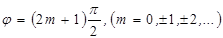. Тогда уравнение (4.15) примет вид

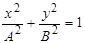. (4.17)

Это есть уравнение эллипса, оси которого совпадают с осями координат, а его полуоси равны, соответственно, А и В. Такие колебания называются эллиптически поляризованными. Если ещё и А=В, то эллипс вырождается в окружность, и колебания в этом случае называются циркулярно-поляризованными. Анализ показывает (провести самостоятельно), что при 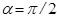точка вращается по часовой стрелке, при 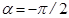– против.

Если частоты складываемых колебаний различны, то замкнутая траектория результирующего колебания имеет сложную форму, которая зависит от соотношения частот и фаз складываемых колебаний. В этом случае результирующие кривые называются фигурами Лиссажу. Эти фигуры протабулированы, и их анализ позволяет делать заключение о характеристиках одного колебания, если характеристики другого известны.