.
Все модели исследования операций могут быть классифицированы в зависимости от природы и свойств операции, характера решаемых задач, особенностей применения математических методов.
Следует отметить прежде всего большой класс оптимизационных моделей. Такие задачи возникают при попытке оптимизировать планирование и управление сложными системами. В первую очередь экономическими системами. Оптимизационную задачу можно сформулировать в общем виде: найти переменные 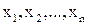 , удовлетворяющие системе неравенств (уравнений)
, удовлетворяющие системе неравенств (уравнений)
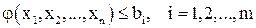 (1)
(1)
и обращающие в максимум (или минимум) целевую функцию, т.е.
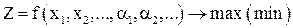 (2)
(2)
(Условия неотрицательности переменных, если они есть, входят в ограничения (1)).Упорядоченная совокупность значений 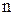 переменных
переменных 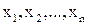 представляется точкой
представляется точкой 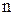 - го пространства. В дальнейшем эту точку будем обозначать
- го пространства. В дальнейшем эту точку будем обозначать 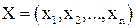 , а само оптимальное решение
, а само оптимальное решение 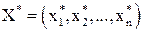 .
.
Это задачи отыскания значений параметров, обеспечивающих экстремум функции при наличии ограничений, наложенных на аргумент.
Если критерий эффективности 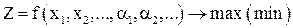 представляет линейную функцию, а функции
представляет линейную функцию, а функции 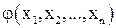 в системе ограничений (1) также линейны, то такая задача является задачей линейного программирования. Если, исходя из содержательного смысла, её решения должны быть целыми числами, то эта задача целочисленного линейного программирования. Если критерий эффективности и (или) система ограничений задаются нелинейными функциями, то имеем задачу нелинейного программирования.
в системе ограничений (1) также линейны, то такая задача является задачей линейного программирования. Если, исходя из содержательного смысла, её решения должны быть целыми числами, то эта задача целочисленного линейного программирования. Если критерий эффективности и (или) система ограничений задаются нелинейными функциями, то имеем задачу нелинейного программирования.
Если в задаче математического программирования имеется переменная времени и критерий эффективности (2) выражается не в явном виде как функция переменных, а косвенно – через уравнения, описывающие протекание операций во времени, то такая задача является задачей динамического программирования.







Определение: Общей задачей линейного программирования называется задача, которая состоит в определении максимального или минимального значения функции:
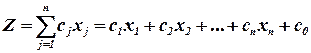 (3)
(3)
при условиях 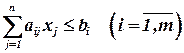 , т.е.
, т.е.
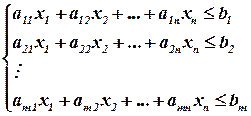 (4)
(4)
Функция 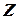 - называется целевой, а условия (4) – ограничениями.
- называется целевой, а условия (4) – ограничениями.
Определение: Совокупность чисел 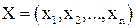 удовлетворяющих ограничения (4) называется допустимым решением или планом.
удовлетворяющих ограничения (4) называется допустимым решением или планом.
Определение: План, 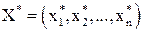 при котором целевая функция (3) принимает своё максимальное или минимальное значение называется оптимальным.
при котором целевая функция (3) принимает своё максимальное или минимальное значение называется оптимальным.
Рассмотрим экономико-математическую модель простейшей задачи линейного программирования (производственное планирование)
 2014-02-02
2014-02-02 2180
2180
