Формы записи вещественных чисел

Вещественные числа могут записываться двумя способами – в общепринятой и экспоненциальной форме. Общепринятая форма предполагает запись по обычным правилам арифметики. Целая часть от дробной отделяется десятичной точкой, а не запятой, как в математике. Если точка отсутствует, число считается целым.

Запись вещественного числа в экспоненциальной форме (в форме с мантиссой и порядком) использует степень десяти (например: 25*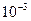) и удобна для записи очень больших и очень маленьких чисел. При этом число изображается так: пишется мантисса, знак умножения опускается, вместо основания 10 пишется буква е, а следом указывается порядок (показатель степени). Буква е, предшествующая порядку, читается как «умножить на 10 в степени».

Например, 123,456 или -11,9 – общепринятая форма, а 5.18е+02(518) или 10е-03(0,01) – экспоненциальная.

Примеры неправильной записи вещественных чисел:

· 123- отсутствует десятичная точка;

· 1,23 - запятая вместо точки;

· 0.123-03 -отсутствует обозначение порядка е;

· 12.34е1.2-порядок числа должен быть целым.

Любое вещественное число хранится в памяти компьютера в экспоненциальной форме: отдельно – мантисса и отдельно – порядок. При этом под мантиссу и порядок отводится строго определенное количество двоичных разрядов. Выбор такого представления имеет несколько следствий:

· Существуют очень маленькие значения (машинное ε – “машинное эпсилон”), которые не могут быть представлены. Попытки их использования обычно приводят к возникновению ошибок;

· Каждое вещественное число будет иметь приблизительно одинаковое количество значащих цифр в его представлении. Как следствие этого, ошибка для очень больших чисел будет больше по абсолютной величине;

· Представители вещественных чисел неравномерно распределены внутри диапазона значений. Их плотность уменьшается с увеличением абсолютного значения числа.

· Вещественные числа представлены приближенно, следовательно, арифметические действия над ними также выполняются приближенно.

Из изложенного следует несколько простых правил:

· Вещественные числа нежелательно проверять на строгое равенство;

· Необходимо проявлять осмотрительность при преобразовании вещественных чисел в целые и избегать вычитания почти равных чисел, т.к. могут возникнуть ошибки из-за потери многих значащих цифр;

· Для уменьшения влияния ошибки округления при выполнении арифметических операций с вещественными числами необходимо иметь в виду следующее. Если складывается много чисел, то их нужно разбить на группы чисел, близких по абсолютному значению, произвести суммирование в группах, начиная с меньшего числа, после чего полученные суммы сложить, опять-таки начиная с меньшей. По аналогии с предыдущим получаются оценки для других арифметических операций и соответствующие практические рекомендации.

Вещественные числа в шестнадцатеричной системе счисления записывать нельзя.