Касательные напряжения при изгибе. Формула Журавского

Рассмотрим задачу об определении касательных напряжений при изгибе для узкого прямоугольника в качестве сечения.

При изгибе Q_у ¹ 0 и М_х ¹ 0. В этом случае в сечении возникают три напряжения s_z, t_zx, t_zy. Тогда уравнения равновесия (54) и (55) из полной математической модели твердо деформированного тела примут следующий вид:

,

,

.

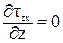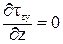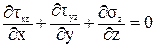Из первых двух уравнений следует, что касательные напряжения являются функцией двух переменных (х, у). так как поверхность стержня свободна от напряжений, то по периметру сечения t_zx = 0 по закону парности касательных напряжений (рис. 37).

Рис. 37

Для узкого прямоугольника они не успевают вырасти, поэтому будем считать t_zx равными нулю по всей ширине сечения. Тогда третье уравнение равновесия примет вид:

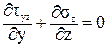. (81)

По той же причине, что прямоугольник узкий, будем считать, что t_zy по ширине сечения при у = const распределено равномерно и является функцией только координаты у:

.

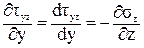Пользуясь формулой нормальных напряжений в поперечном сечении (28), при изгибе получим:

s = ,

=,

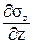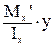М_х’ = Q_y

.

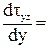
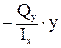Проинтегрировав полученное выражение, получим:

t_zy=-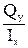×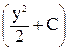. (82)

Постоянную интегрирования можно определить из условия равенства нулю касательного напряжения t_zy при у=: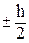

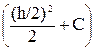=0,

С = -.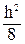

Подставив значение константы в выражение (82) получим:

t_zy = - 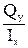×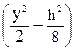= 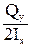×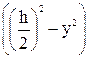. (83)

На основе выражения в скобках можно сделать вывод, что касательные напряжения в сечении распределены по параболе.

Рис. 38

Преобразуем выражение в скобках:

×=××.

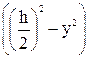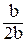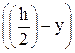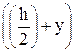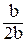На рисунке 38 координатой y отсекается заштрихованная часть, которая имеет площадь F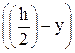^*=×b и координату центра тяжести относительно оси х у_с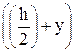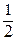^*=×. Произведение площади фигуры на координату ее центра тяжести относительно какой-либо оси дает статический момент инерции S_x^*. Таким образом, выражение (83) примет вид:

t_zy= 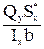. (84)

Эта формула носит название формулы Журавского и служит для определения касательных напряжений, возникающих в сечении при изгибе.