Переменное электрическое поле порождает магнитное, которое тоже является переменным. Это переменное магнитное поле порождает электрическое и т.д. Таким образом, если возбудить с помощью колеблющихся зарядов переменное электромагнитное поле, то в окружающем заряды пространстве возникнет последовательность взаимных превращений электрического и магнитного полей, распространяющихся от точки к точке. Этот процесс будет периодическим во времени и пространстве, и, следовательно, представляет собой волну.
 Опр. 2.1. Электромагнитными волнами называется распространяющееся в пространстве с конечной скоростью переменное электромагнитное поле.
Опр. 2.1. Электромагнитными волнами называется распространяющееся в пространстве с конечной скоростью переменное электромагнитное поле.
При рассмотрении э/м волн речь идет о колебаниях векторов напряженности электрического (Е) и магнитного (Н) полей. Эти колебания взаимно обусловлены: изменяющееся во времени магнитное поле порождает изменяющееся во времени электрическое поле, которое, в свою очередь, порождает изменяющееся во времени магнитное поле…и т. д. Связь между 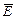 и
и 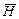 , а также их зависимость от координат и времени определяется системой дифференциальных уравнений Максвелла для электромагнитного поля. Само существование электромагнитных волн вытекает из уравнений Максвелла.
, а также их зависимость от координат и времени определяется системой дифференциальных уравнений Максвелла для электромагнитного поля. Само существование электромагнитных волн вытекает из уравнений Максвелла.
|

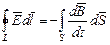
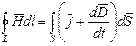


Связь между величинами: 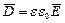 ;
; 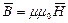 ;
; 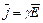 , где
, где  и
и 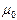 — соответственно электрическая и магнитная постоянные,
— соответственно электрическая и магнитная постоянные, 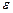 и
и 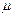 — электрическая и магнитная проницаемости среды.
— электрическая и магнитная проницаемости среды.
|
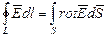 , где
, где 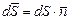 , можно записать полную систему уравнений Максвелла в дифференциальной форме:
, можно записать полную систему уравнений Максвелла в дифференциальной форме: 



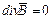
Каждое из векторных уравнений эквивалентно трем скалярным уравнениям, связывающим компоненты векторов, стоящих в левой и правой частях равенств. Из первого получаем: 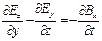 ,
, 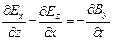 ,
,  ,
,
|
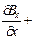
 .
. Из второго: 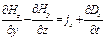 ,
, 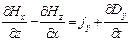 ,
, 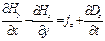 , из второго и третьего:
, из второго и третьего: 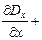


|
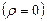 нейтральной
нейтральной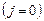 среды с постоянными проницаемостями
среды с постоянными проницаемостями 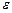 и
и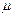 , получаем:
, получаем: 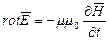


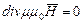
Продифференцировав обе части первого уравнения Максвелла по координатам и времени, получаем:  , т.к.
, т.к. 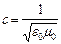 - скорость света в вакууме, то
- скорость света в вакууме, то 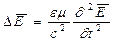 . Аналогично
. Аналогично 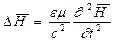 , где
, где 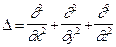 - оператор Лапласа.
- оператор Лапласа.
Полученные уравнения – типичные волновые уравнения. Всякая функция, удовлетворяющая такому уравнению, описывает некоторую волну, фазовая скорость которой 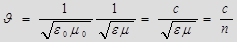 , (2.5)
, (2.5)
где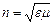 - показатель преломления среды. В вакууме (
- показатель преломления среды. В вакууме (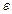 =1 и
=1 и 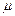 = 1) скорость распространения э/м волн совпадает со скоростью с. Это навело Максвелла на мысль об электромагнитной природе света. Так как в среде
= 1) скорость распространения э/м волн совпадает со скоростью с. Это навело Максвелла на мысль об электромагнитной природе света. Так как в среде 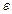 >1,
>1,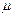 > 1, то скорость распространения электромагнитных волн в веществе всегда меньше, чем в вакууме.
> 1, то скорость распространения электромагнитных волн в веществе всегда меньше, чем в вакууме.
 Опр. 2.2. Фазовая скорость – скорость распространения волны
Опр. 2.2. Фазовая скорость – скорость распространения волны
Тогда из уравнений Максвелла следует, что вектора напряженности Е и Н переменного электромагнитного поля удовлетворяют волновому уравнению типа:

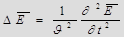 ,
, 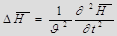 (2.6)
(2.6)
Раскрыв оператор Лапласа, получим:
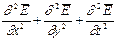
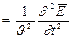 и
и 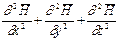
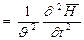
 Опр. 2.3. Электромагнитная волна называется плоской, если векторы Е и Н зависят только от времени и одной декартовой координаты, например от х. В плоской волне все лучи параллельны друг другу.
Опр. 2.3. Электромагнитная волна называется плоской, если векторы Е и Н зависят только от времени и одной декартовой координаты, например от х. В плоской волне все лучи параллельны друг другу.
Пусть плоская электромагнитная волна распространяется в нейтральной непроводящей среде. Линии, вдоль которых распространяется энергии, называются лучами. Световой луч – направление распространения световой волны. Направим ось 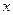 перпендикулярно к волновым поверхностям. Тогда
перпендикулярно к волновым поверхностям. Тогда 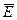 и
и 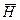 , а значит, и их компоненты по координатным осям не будут зависеть от координат
, а значит, и их компоненты по координатным осям не будут зависеть от координат 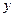 и
и 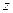 . Поэтому уравнения Максвелла в скалярной упрощаются следующим образом:
. Поэтому уравнения Максвелла в скалярной упрощаются следующим образом:
|
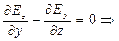
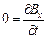
 (1);
(1); 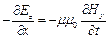 (2);
(2); 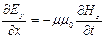 (3),
(3), 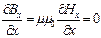 (4)
(4) 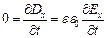 (5),
(5), 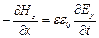 (6),
(6), 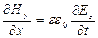 (7),
(7), 
 (8)
(8) Исходя из уравнений (4) и (8): и
и 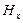 не зависят ни от
не зависят ни от 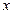 , ни от
, ни от 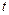 . Следовательно, отличные от нуля
. Следовательно, отличные от нуля 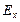 и
и 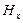 могут быть обусловлены лишь постоянными однородными полями, накладывающимися на электромагнитное поле волны. Само поле волны не имеет составляющих вдоль оси
могут быть обусловлены лишь постоянными однородными полями, накладывающимися на электромагнитное поле волны. Само поле волны не имеет составляющих вдоль оси 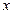 . Т.о. векторы
. Т.о. векторы 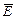 и
и 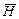 перпендикулярны к направлению распространения волны, т.е. что электромагнитные волны поперечны. В дальнейшем мы будем предполагать постоянные поля отсутствующими и полагать
перпендикулярны к направлению распространения волны, т.е. что электромагнитные волны поперечны. В дальнейшем мы будем предполагать постоянные поля отсутствующими и полагать  =
=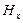 = 0.
= 0.

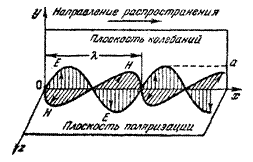 Опр. 2.4. Плоскость, проведенная через вектор Е и световой луч, называется плоскостью колебаний линейно поляризованной волны.
Опр. 2.4. Плоскость, проведенная через вектор Е и световой луч, называется плоскостью колебаний линейно поляризованной волны.
Опр. 2.5.Плоскостью поляризации называется плоскость, проведенная через вектор Н и световой луч.
Исходя из уравнений (3) и (6): если первоначально было создано переменное электрическое поле 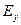 , направленное вдоль оси
, направленное вдоль оси 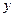 (3), то это поле создаст магнитное поле
(3), то это поле создаст магнитное поле  (6), направленное вдоль оси
(6), направленное вдоль оси 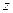 . В соответствии с (3) поле
. В соответствии с (3) поле  создаст электрическое поле
создаст электрическое поле 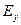 , и т.д. Ни поле
, и т.д. Ни поле 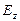 , ни поле
, ни поле 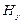 при этом не возникают.
при этом не возникают.
Аналогично для уравнений (2) и (7) возникает поле 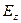 -
- 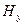 , а поле
, а поле 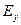 -
- не возникает. Т.о. для описания плоской электромагнитной волны достаточно взять одну из пар уравнений, положив компоненты, фигурирующие во второй, равными нулю.
не возникает. Т.о. для описания плоской электромагнитной волны достаточно взять одну из пар уравнений, положив компоненты, фигурирующие во второй, равными нулю.
Плоскости колебаний и поляризации взаимно перпендикулярны.
Пусть 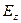 =
=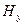 =0. Продифференцируем уравнение (3) по
=0. Продифференцируем уравнение (3) по 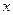 :
: 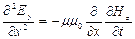 , где
, где 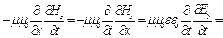
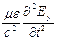 - волновое уравнение для
- волновое уравнение для 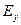 . Аналогично из уравнения (6):
. Аналогично из уравнения (6): 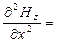
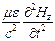 .
.
|
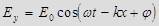 ,
,  ,
,
где E0 и H0 — соответственно амплитуды напряженностей электрического и магнитного полей волны, 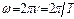 - круговая частота волны,
- круговая частота волны, 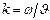 — волновое число,
— волновое число, 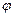 — начальные фазы колебаний в точках с координатой х=0,x- пройденное волной расстояние. В уравнениях
— начальные фазы колебаний в точках с координатой х=0,x- пройденное волной расстояние. В уравнениях 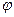 одинаково, так как колебания электрического и магнитного векторов в электромагнитной волне происходят с одинаковой фазой.
одинаково, так как колебания электрического и магнитного векторов в электромагнитной волне происходят с одинаковой фазой.
Подставим эти решения в уравнения (3) и (6):

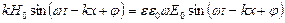 ,
,
получаем 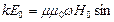 и
и 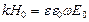 . Перемножим эти два выражения:
. Перемножим эти два выражения: 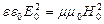 . Т.к.
. Т.к. 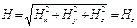 (
( , а в нашем случае
, а в нашем случае 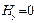 ) и
) и 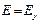 , то
, то 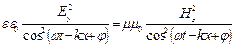 и
и 
Следствия теории Максвелла:
1. Э/м волны являются поперечными: векторы Е и Н взаимно перпендикулярны (направлены вдоль оy и оz; рис. - моментальная «фотография» плоской э/м волны) и лежат в плоскости, перпендикулярной к вектору 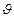 скорости распространения волны.
скорости распространения волны.
2. Векторы 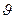 , Е и Н образуют правовинтовую систему: из конца вектора
, Е и Н образуют правовинтовую систему: из конца вектора 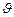 враще-ние от Е к Н по кратчайшему расстоянию видно происходящим против часовой стрелки.
враще-ние от Е к Н по кратчайшему расстоянию видно происходящим против часовой стрелки.
3. Векторы Е и Н всегда колеблются в одинаковых фазах в электромагнитной волне (рис.), причем мгновенные значения Е и Н в любой точке связаны соотношением:
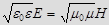 (2.9)
(2.9)
для вакуума 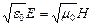 (2.9’)
(2.9’)
Следовательно, Е и Н одновременно достигают максимума, одновременно обращаются в нуль и т. д.
 Опр. 2.6. Электромагнитная волна называется монохроматической, если компоненты векторов Е и Н электромагнитного поля волны совершают гармонические колебания одинаковой частоты, называемой частотой волны. Монохроматическая волна неограниченна в пространстве и времени.
Опр. 2.6. Электромагнитная волна называется монохроматической, если компоненты векторов Е и Н электромагнитного поля волны совершают гармонические колебания одинаковой частоты, называемой частотой волны. Монохроматическая волна неограниченна в пространстве и времени.
Утверждение, что свет - поперечные электромагнитные волны, основано на результатах огромного числа экспериментальных исследований дифракции, интерференции и поляризации света и распространения света в анизотропных средах. Так как векторы Е и Н взаимно перпендикулярны, то для описания закономерностей поляризации света достаточно знать поведение лишь одного из векторов. Обычно все рассуждения ведутся относительно светового вектора.
 Опр. 17.1. Световой вектор — вектор напряженности Е электрического поля (это название обусловлено тем, что при действии света на вещество основное значение имеет электрическая составляющая поля волны, действующая на электроны в атомах вещества).
Опр. 17.1. Световой вектор — вектор напряженности Е электрического поля (это название обусловлено тем, что при действии света на вещество основное значение имеет электрическая составляющая поля волны, действующая на электроны в атомах вещества).
Световую волну можно описать как 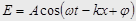 , где А – амплитуда.
, где А – амплитуда.
Характеристикой волны является 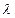 :
: 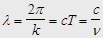 (2.10)
(2.10)
 Опр. 2.7. Длина волны (
Опр. 2.7. Длина волны (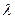 ) - минимальное расстояние между двумя точками пространства или среды, колебания векторов напряженности электрического поля (или векторов напряженности магнитного поля) в которых совершаются в одинаковой фазе.
) - минимальное расстояние между двумя точками пространства или среды, колебания векторов напряженности электрического поля (или векторов напряженности магнитного поля) в которых совершаются в одинаковой фазе.
В среде: 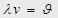 (2.11)
(2.11)
В вакууме: 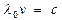 (2.11’)
(2.11’)
Если э/м волна с частотой 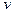 переходит из вакуума в среду с абсолютным показателем преломления n, то ее частота остается неизменной, а длина волны считается равной:
переходит из вакуума в среду с абсолютным показателем преломления n, то ее частота остается неизменной, а длина волны считается равной:
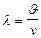 ,
, 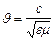 ,
, 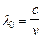 . Тогда
. Тогда 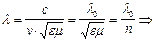
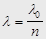 (2.12)
(2.12)
Произвольная немонохроматическая волна может быть представлена в виде совокупности монохроматических волн.
Длины волн видимого света: 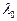 = 0,40 — 0,76 мкм (4000 — 7600Å). Эти значения относятся к световым волнам в вакууме. В веществе длины световых волн будут иными. Частоты видимых световых волн лежат в пределах: v =(0,39-0,75)-1015 Гц
= 0,40 — 0,76 мкм (4000 — 7600Å). Эти значения относятся к световым волнам в вакууме. В веществе длины световых волн будут иными. Частоты видимых световых волн лежат в пределах: v =(0,39-0,75)-1015 Гц
Белый свет – набор длин волн от 4000 до 7600Å.
 2014-02-03
2014-02-03 11239
11239