Противоречие между статической точностью регулирования и устойчивостью

Рассмотрим систему стабилизации частоты вращения вала двигателя с центробежным регулятором прямого действия, имеющую следующее математическое описание:

(Tp + 1)y = k_xx - k_zz

(T₂²p² + T₁p + 1)x = -k_py. (9.1)

Исключив из этой системы уравнений х, получим ДУ САР:

[(Tp+1)(T₂²p²+T₁p+1)+k_xk_p]y = -k_z(T₂²p²+T₁p+1)z,

или, после преобразований,

[TT₂²p³+(TT₁+T₂²)p²+(T+T₁)p+(1+k_xk_p)]y = -k_z(T₂²p²+T₁p+1)z. (9.2)

Условие установившегося режима при возмущении z=z₀ получим, потребовав, чтобы р =0:

(1+k_xk_p)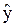= -k_zz₀,

откуда

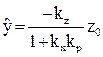. (9.3)

Очевидно, что для уменьшения статической ошибки по модулю следует увеличивать коэффициент усиления регулятора k_p.

Рассмотрим характеристическое уравнение САР

TT₂²p³+(TT₁+T₂²)p²+(T+T₁)p+(1+k_xk_p)=0.

Условие устойчивости имеет вид

(TT₁+T₂²)(T+T₁) > TT₂² (1+k_xk_p),

откуда

k_p < 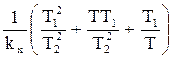. (9.4)

Оказывается, что, с одной стороны, согласно (9.3) коэффициент усиления регулятора нужно увеличивать, а с другой стороны, по условиям устойчивости он ограничен сверху. Очевидно, что условие устойчивости накладывает ограничение снизу на величину статической ошибки.

Покажем, что описанное ограничение распространяется на системы любого порядка. Пусть собственный оператор САР имеет вид

D(p) = a_npⁿ + a_n-1p^n-1 +…+ a₁p + a₀.

Как следует из предыдущих рассуждений, коэффициент a₀ = 1+k_xk_p. Применив критерий Михайлова, получим выражения для компонент вектора кривой Михайлова:

U = a₀ – a₂w² + a₄w⁴ – a₆w⁶ +…

V = a₁w - a₂w³ + a₅w⁵ –a₇w⁷ +…

Предположим, что система при некотором значении а₀ была устойчивой (рис.9.1, кривая а). Очевидно, что при увеличении k_p увеличивается а₀, и кривая Михайлова смещается вправо, так что при некотором достаточно большом а₀ она не пройдёт через вторую либо третью четверти (рис.9.1, кривая б), а это означает потерю устойчивости системой.

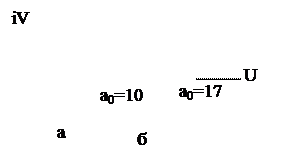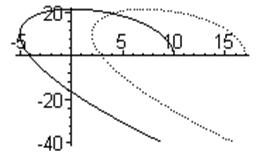
Рис.9.1. Потеря устойчивости при слишком больших

коэффициентах усиления регулятора.

Рекомендуемая литература

1. Бесекерский В.А., Попов Е.В. Теория систем автоматического регулирования. М.: Наука, 1972.- 767 с.

2. Воронов А.А. Основы теории автоматического управления. Ч.1. М.: Энергия, 1965.- 396 с.

3. Воронов А.А. Основы теории автоматического управления. Ч.2. М.: Энергия, 1966.- 384 с.

4. Гитис Э.И., Данилович Г.А., Самойленко В.И. Техническая кибернетика. М.: Советское радио, 1969.- 486 с.

5. Под ред. Пономарёва В.М. и Литвинова А.П. Основы автоматического регулирования и управления. М.: Высшая школа, 1974.- 439 с.

6. Под ред. Солодовникова В.В. Техническая кибернетика. Книга 1.- 768 с., Книга 2.- 679 с., Книга 3, Ч.1.- 607 с.,Ч.2.- 367 с. М.: Машиностроение, 1967 – 1968.

7.Юревич Е.И. Теория автоматического управления. Л.: Энергия, 1975.- 404 с.