Динамические характеристики линейных систем

Прежде чем изучать поведение реальных систем и их моде­лей, необходимо определить формальный язык, на котором будут обсуждаться их свойства. Основным элементом такого фор­мального языка является понятие динамических характеристик, под которыми интуитивно понимают какие-либо соотношения, ха­рактеризующие свойства систем в статике и динамике (при изме­нении состояния).

Дадим следующее определение. Динамической характери­стикой (математической моделью) системы будем называть любое соотношение, заданное аналитически, графически или в виде таб­лицы, которое позволяет оценить ее поведение во времени.

В этом разделе мы будем рассматривать различные способы описания линейных динамических систем, их взаимосвязь и при­ведение к принятой в теории автоматического управления форме записи математической модели.

Отметим, что динамическая характеристика дает возможность исследовать поведение системы, т. е. рассчитать для нее переход­ные процессы.

Дифференциальные уравнения

Наиболее часто в качестве математической модели объекта управления используются обыкновенные дифференциальные урав­нения, которые могут быть записаны в различной форме.

Линейные многоканальные объекты обычно описывают систе­мой дифференциальных уравнений первого порядка, представлен­ной в векторно-матричном виде:

х = Ах + Ви (2.1.)

Здесь хЄ Rⁿ - вектор состояния, п - порядок объекта; иЄ Rm -вектор управляющих воздействий, т≤п; А - квадратная матрица действительных коэффициентов; В - прямоугольная матрица дей­ствительных коэффициентов. Уравнения (2.1) называют диффе­ренциальными уравнениями состояния.

Выходные переменные объекта изменяются в соответствии с уравнением выхода

У = Сх, (2.2)

где yЄ Rm - вектор выхода; С - прямоугольная матрица действи­тельных коэффициентов. Уравнения (2.1) и (2.2) описывают ли­нейный многоканальный объект.

Для описания одноканального объекта обычно используется скалярное дифференциальное уравнение:

у^(п) + а_пу^﴾n-1) +... + а₂у + а₁у = bи, (2.3)

которое также может быть приведено к виду (2.1) и (2.2) после со­ответствующего выбора линейно-независимых переменных со­стояния. Их число всегда равно порядку объекта (n), a uЄR¹ и уЄ R¹.

Наиболее простое каноническое описание получается в случае, когда в качестве переменных состояния выбираются выходная пе­ременная у и ее производные до (п -1) включительно

х₁=у, х₂=у,..., х_n=у^(n-1).

При этом вместо (2.3) имеем систему уравнений

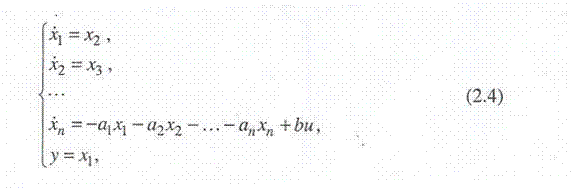которая соответствует векторно-матричным уравнениям (2.1) и (2.2). Здесь матрицы А, В и С имеют вид

Выбрав соответствующие переменные состояния, от описания (2.5) также можно перейти к векторно-матричным уравнениям типа (2.1), (2.2). Рассмотрим этот переход на примере.

Пример 2.2

Записать уравнения состояния объекта с математической моде­лью вида

Таким образом, в качестве основной динамической характе­ристики линейных объектов управления используются диффе­ренциальные уравнения, которые могут быть представлены в форме (2.1), (2.2).

В теории автоматического управления рассматриваются не фи­зические системы управления, а их математические модели, по­этому необходимо стремиться к тому, чтобы эта модель достаточ­но адекватно отражала свойства реального устройства. Процедуру получения математической модели объекта можно разбить на сле­дующие этапы:

Составление гносеологической (мысленной) модели объекта. Исходя из технического задания и изучения режимов работы объ­екта инженер создает приближенную мысленную модель, которая в дальнейшем уточняется и приобретает вид математической модели.

Определение независимых переменных, которые характеризуют объект, и уточнение их размерностей. При этом число управляю­щих воздействий не может быть меньше числа выходных перемен­ных (dim u ≥dim у). Размерность вектора переменных состояния не может быть меньше размерности вектора выходных перемен­ных (dim u ≥ dim y). Размерность возмущающих воздействий М может быть произвольной и никак не связана с размерностью у, х, и.

Запись физических законов, в силу которых развиваются про­цессы в объекте.

Приведение уравнений объекта к удобному с точки зрения тео­рии автоматического управления виду.

Математическая модель никогда не бывает, тождественна рас­сматриваемому объекту, так как при ее составлении всегда делают какие-либо допущения и упрощения. Поэтому для одной и той же системы в зависимости от целей управления модели могут быть различными.

При составлении математической модели приходится искать компромиссный вариант между двумя противоречивыми требова­ниями: с одной стороны, модель должна наиболее полно отражать свойства реальной системы, с другой - быть простой, чтобы не за­труднять исследований.

Перейдем к удобному с точки зрения теории управления описа­нию объекта. При этом выходной величиной будем считать напря­жение на выходе цепи, т. е. y = U₂, управляющим воздействием -напряжение на ее входе (u=U₁), а переменной состояния- ток, протекающий по цепи (х=1). С учетом

Здесь ф - угол отклонения маятника (выходная переменная); U - прикладываемая управляющим двигателем сила (входная пере­менная); s - перемещение каретки; m₁ - масса каретки; L - расстоя­ние между осью и центром тяжести маятника; m₂ - масса маятника; J - момент инерции относительно центра тяжести; g - ускорение си­лы тяжести; Н и V - горизонтальная и вертикальная силы реакции у оси маятника.

Упрощенная модель объекта «каретка - маятник» может быть представлена системой дифференциальных уравнений [9]

Для аналитического определения переходной функции следует решить дифференциальное уравнение при нулевых начальных ус­ловиях и единичном входном воздействии.

При исследовании реального объекта переходную характери­стику можно получить экспериментальным путем, подавая на его вход ступенчатое воздействие и фиксируя реакцию на выходе. Ес­ли входное воздействие представляет собой неединичную ступен­чатую функцию u(t)= к 1 (t), то выходная величина будет равна y(l) = k h(t), т. е. представляет собой переходную характеристику с коэффициентом пропорциональности k.

Зная переходную характеристику, можно вычислить реакцию системы на произвольное входное воздействие с помощью инте­грала свертки

y(t) = h(t)u(t) +∫ h(t - x)u(τ)dτ (2.6)

(τ- переменная интегрирования).

2.4. ИМПУЛЬСНАЯ ПЕРЕХОДНАЯ ФУНКЦИЯ

Эта характеристика также используется для описания одноканальных объектов вида (2.5).

Импульсная переходная функция (характеристика) g(t) пред­ставляет собой реакцию на входное воздействие типа единичной импульсной функции при нулевых начальных условиях (рис. 2.5).

Такое входное воздействие математически отражает дельта-функция, которая обладает следующими свойствами:

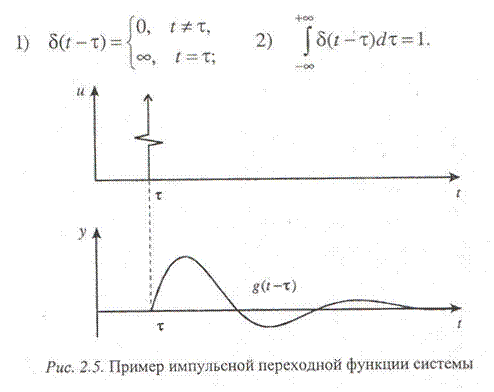С помощью дельта-функции можно описать реальное входное воздействие типа удара. В действительности импульсные входные воздействия на объект всегда конечны по уровню и продолжитель­ности. Однако если их длительность намного меньше длительно­сти переходных процессов, то с определенной точностью реальный импульс может быть заменен дельта-функцией с некоторым коэф­фициентом.

Импульсная переходная функция позволяет вычислить реакцию системы на произвольное входное воздействие при нулевых на­чальных условиях по выражению

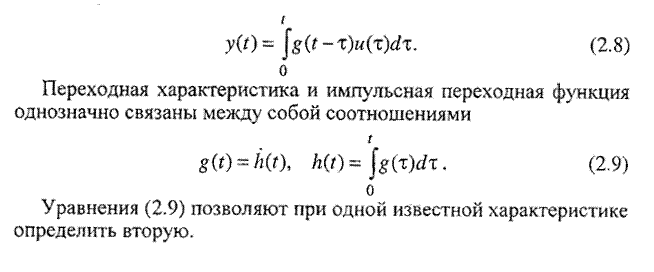Если система имеет нулевые начальные условия х(0)=0, то выражение (2.14) принимает вид:

При небольших размерах или простой структуре матрицы объ­екта А выражение (2.18) может быть использовано для точного представления переходной матрицы с помощью элементарных функций. В случае большой размерности матрицы А следует ис­пользовать существующие программы для вычисления матричного экспоненциала.

2.6. ПЕРЕДАТОЧНАЯ ФУНКЦИЯ

Наряду с обыкновенными дифференциальными уравнениями в теории автоматического управления используются различные их преобразования. Для линейных систем эти уравнения удобнее представлять в символической форме с применением так называе­мого оператора дифференцирования

р=d/ dt

что позволяет записывать дифференциальные уравнения как алгебраические и вводить новую динамическую характеристику -передаточную функцию. Этот способ был предложен английским ученым Хевисайдом в 1895 г., позднее он был строго обоснован аппаратом интегральных преобразований Лапласа и Карсона [4] в предположении нулевых начальных условий.

Рассмотрим этот переход для многоканальных систем общего вида

Чаще всего передаточные функции применяются для описания одноканальных систем вида (2.5)

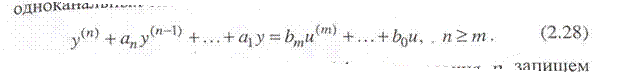
С использованием оператора дифференцирования р запишем уравнение (2.28) в символической форме и найдем передаточную функцию как отношение выходной величины к входной:

Передаточную матрицу (передаточную функцию) можно также определить с помощью изображений Лапласа или Карсона - Хеви-сайда. Если подвергнуть одному из этих преобразований обе части дифференциального уравнения и найти соотношения между вход­ными и выходными величинами при нулевых начальных условиях, то получим ту же самую передаточную матрицу (2.24) или функ­цию (2.29).

Все динамические характеристики объекта взаимосвязаны: по­лучив одну из них, можно определить все остальные. Мы рассмот­рели переход от дифференциальных уравнений к передаточным функциям с помощью оператора дифференцирования р. Используя этот оператор, несложно перейти от передаточной функции к сим­волической форме записи дифференциального уравнения, а затем к стандартному описанию объекта в форме (2.3) или (2.5).

Обсудим теперь взаимосвязь между переходными характери­стиками и передаточной функцией. С этой целью запишем выражение для выходной переменной объекта через импульсную пере­ходную функцию в соответствии с (2.8)

Определить передаточную функцию двигателя постоянного тока с независимым возбуждением (см. рис.2.2).

Дифференциальное уравнение двигателя получено в при­мере 2.4 и имеет вид

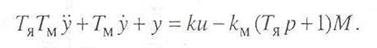Будем полагать, что возмущающее воздействие отсутствует, т. е. М = 0. Запишем это уравнение в символической форме с помо­щью оператора дифференцирования р

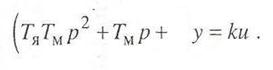или, рассматривая его как алгебраическое,

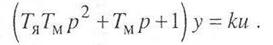Определим теперь передаточную функцию двигателя постоян­ного тока с независимым возбуждением

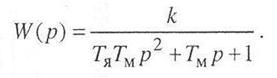Как видим, она не содержит нулей и имеет два полюса, которые в зависимости от численных значений параметров Т_я и Г_м могут быть вещественными или комплексно-сопряженными

2.7. МОДАЛЬНЫЕ ХАРАКТЕРИСТИКИ

Модальные характеристики соответствуют свободной состав­ляющей движения системы (2.1) или, другими словами, отражают свойства автономной системы (2.10)