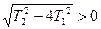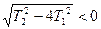Пример
Пример
Пример
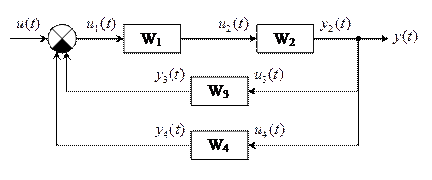
Решение:
Заменим последовательные звенья 1 и 2 на звено 12:
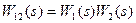 ;
;
Заменим параллельные звенья 3 и 4 на звено 34:
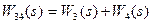 ;
;
Найдем передаточную функцию всей системы:
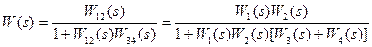 .
.
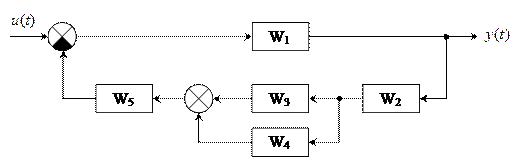
Решение:
Заменим параллельные звенья 3 и 4 на звено 34:
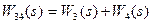 ;
;
Замени последовательные звенья 3, 34 и 5 на звено 2345:
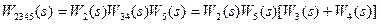 ;
;
Найдем передаточную функцию всей системы:
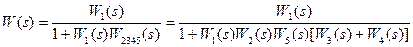 .
.
Построить временные и частотные характеристики для элементарного звена 2-го порядка дифференциальное уравнение которого:
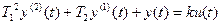 .
.
Рассмотреть:
Решение:
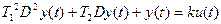 ;
;
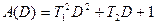 ;
;
 ;
;
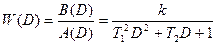 ;
;
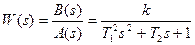 .
.
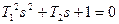 ;
;
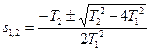 .
.
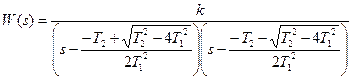 .
.
Рассмотрим временные характеристики:
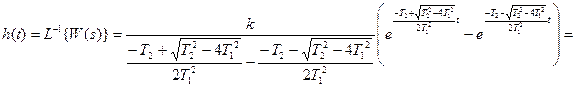
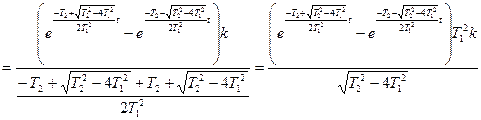 .
.
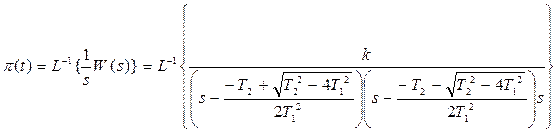 ;
;
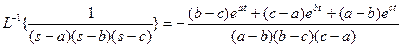 ;
;
 .
.
Комплексная частотная характеристика:
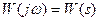
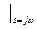 ;
;
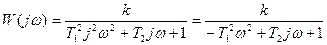 .
.
Термин пространства состояний получил широкое распространение в ТАУ для описания динамики систем во временной области. Этот термин является новым названием различных математических процедур, которые ранее использовались в аналитической динамике, квантовой механике, теории устойчивости.
Применение этого метода в ТАУ было определено работами Понтрягина, Беллмана (метод динамического программирования), Калмана.
Метод пространства состояний обладает рядом преимуществ при решении задач многомерных и сложных систем:
- четкая формализация в постановке различных задач в управлении;
- возможность решения задач с большим числом управляемых и управляющих переменных;
- простота алгоритмизации вычислительных процедур;
- ясность (наглядность) математических формулировок при решении задач.
В методе пространства состояний динамика системы представляется зависимостью между тремя множествами переменных 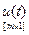 ,
, 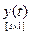 ,
, 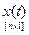 . Вход системы выражается либо множеством временных функций
. Вход системы выражается либо множеством временных функций 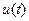 , либо множеством временных последовательностей для дискретных систем
, либо множеством временных последовательностей для дискретных систем 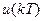 ,
, 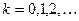 . Выход системы
. Выход системы 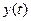 представляет собой описание непосредственно наблюдаемого поведения системы.
представляет собой описание непосредственно наблюдаемого поведения системы.
Основное свойство любой динамической системы заключается в том, что ее поведение в любой момент времени зависит не только от переменных действующих на нее в данный момент времени (от пары 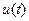 ,
, 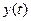 ), но и от переменных действующих на нее в прошлом (
), но и от переменных действующих на нее в прошлом ( ,
, 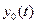 ), т.е. система обладает памятью, позволяющей учитывать вклад переменной, действующей на нее в прошлые моменты времени до наблюдения ее поведения.
), т.е. система обладает памятью, позволяющей учитывать вклад переменной, действующей на нее в прошлые моменты времени до наблюдения ее поведения.
Математическое описание динамической системы времени приводит к подчеркиванию и формализации в направлении причинности от прошлого к будущему.
Поведение и свойства динамической системы можно охарактеризовать понятием состояния системы, которому соответствует определенная точка в евклидовом пространстве с координатами, являющимися координатами состояния. Размерность пространства равна порядку системы дифференциальных уравнений, описывающих ее поведение.
Движение конца вектора состояний в пространстве состояний называется траекторией конца вектора состояний.
В пространстве состояний координатами вектора состояний 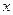 являются переменные системы уравнений, записанные в нормальной форме Коши. (Описание системы дифференциальных уравнений 1-ого порядка называется описанием в нормальной форме Коши). Число векторов определяет порядок системы при этом координаты вектора состояний необязательно соответствуют реальным физическим величинам.
являются переменные системы уравнений, записанные в нормальной форме Коши. (Описание системы дифференциальных уравнений 1-ого порядка называется описанием в нормальной форме Коши). Число векторов определяет порядок системы при этом координаты вектора состояний необязательно соответствуют реальным физическим величинам.
Описание системы в нормальной форме Коши является первичной моделью в системе пространства состояний.
Связь между 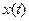 и
и 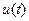 :
:
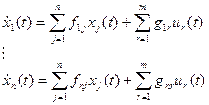
Связь между 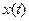 и
и 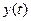 :
:
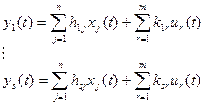 ‚
‚
Система 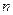 - дифференциальных уравнений и система
- дифференциальных уравнений и система  - алгебраических уравнений ‚ является математической моделью САУ в скалярной форме в пространстве состояний:
- алгебраических уравнений ‚ является математической моделью САУ в скалярной форме в пространстве состояний:
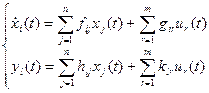 , где
, где
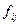 ,
, 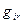 ,
, 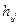 ,
, 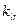 – параметры системы;
– параметры системы;
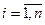 ;
;
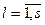 .
.
Другой формой описания САУ в пространстве состояний является векторно-матричная форма, которая имеет вид:
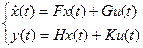 , где
, где
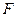 – матрица динамики системы
– матрица динамики системы 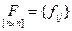 ;
;
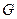 – матрица входа
– матрица входа 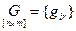 ;
;
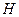 – матрица выхода
– матрица выхода 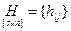 ;
;
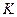 – матрица усиления по входу
– матрица усиления по входу 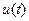
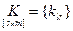 .
.
Уравнение динамики системы (эквивалентно уравнению ):
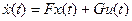 ƒ
ƒ
Уравнение выхода:
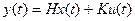 „
„
Вся информация о свойствах системы содержится в числовых таблицах – матрицах параметрах. При анализе и синтезе САУ можно опираться на стандартные преобразования этих таблиц.
Используя представления ƒ и „ или и ‚ можно определить САУ следующим образом:
- САУ называется детерминированной, если ее выход и состояние в произвольный момент времени
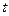 можно достоверно определить по ее состоянию в некоторый момент времени
можно достоверно определить по ее состоянию в некоторый момент времени 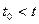 и по известному входу на интервале
и по известному входу на интервале 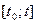 ;
; - Система называется стохастической, если информация о ее состоянии в некоторый момент времени
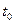 и о ее входе на интервале
и о ее входе на интервале 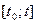 позволяет определить выход и состояние системы в момент времени
позволяет определить выход и состояние системы в момент времени 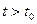 только с определенной вероятностью или другими статистическими методами или средствами;
только с определенной вероятностью или другими статистическими методами или средствами; - Система является физически реализуемой, если ее выход и состояние в произвольный момент времени
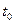 является функцией только тех входов, которые воздействуют на систему до момента
является функцией только тех входов, которые воздействуют на систему до момента 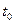 .
.
 2014-02-02
2014-02-02 3521
3521