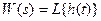
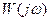 – является преобразованием Фурье от весовой функции
– является преобразованием Фурье от весовой функции 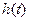 :
:
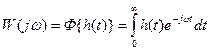 ;
;
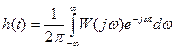
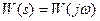
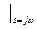
Комплексная частотная характеристика является комплексной величиной.
Комплексная частотная характеристика как и передаточная функция есть отношение выходного гармонического сигнала 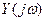 к гармоническому сигналу на входе
к гармоническому сигналу на входе 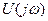 комплексном виде, принимающую множество значений в зависимости от частоты гармонического сигнала
комплексном виде, принимающую множество значений в зависимости от частоты гармонического сигнала 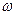 .
.
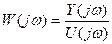 ;
; 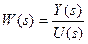 .
.
Представление в полярных координатах:
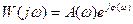 , где
, где
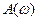 называется амплитудно-частотной характеристикой системы и представляет собой отношение амплитуды гармонического сигнала на выходе
называется амплитудно-частотной характеристикой системы и представляет собой отношение амплитуды гармонического сигнала на выходе 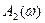 к амплитуде гармонического сигнала на входе
к амплитуде гармонического сигнала на входе 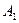 , при частоте входного сигнала равной
, при частоте входного сигнала равной 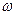 , что означает, что если
, что означает, что если 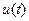 – некоторая амплитуда
– некоторая амплитуда
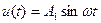 , то
, то
сигнал на выходе
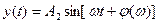
зависит от частоты.
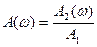 .
.
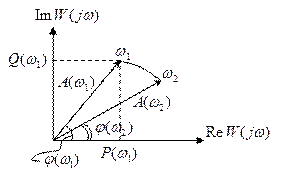
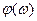 – фазо-частотная характеристика показывает на сколько выходной сигнал
– фазо-частотная характеристика показывает на сколько выходной сигнал 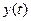 при заданной частоте
при заданной частоте 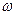 сдвинут по фазе относительно входного сигнала
сдвинут по фазе относительно входного сигнала 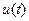 .
.
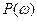 – вещественная часть комплексной частотной характеристики системы;
– вещественная часть комплексной частотной характеристики системы;
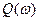 – мнимая часть комплексной частотной характеристики системы.
– мнимая часть комплексной частотной характеристики системы.
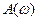 и
и 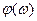 – полярные координаты частотной характеристики.
– полярные координаты частотной характеристики.
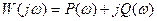
Между полярными координатами и 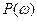 ,
, 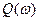 существует однозначное соответствие:
существует однозначное соответствие:
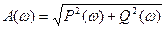 ;
;
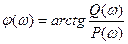 ;
;
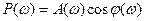 ;
;
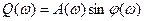 .
.
При каждом фиксированном значении частоты 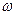 значение
значение 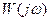 однозначно определяет точку на комплексной области … с декартовыми координатами
однозначно определяет точку на комплексной области … с декартовыми координатами 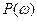 и
и 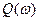 или полярными координатами
или полярными координатами 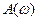 и
и 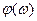 .
.
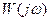 можно изобразить на комплексной области в виде годографа вектора
можно изобразить на комплексной области в виде годографа вектора 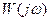 в зависимости от частоты
в зависимости от частоты 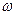 , где
, где 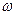 изменяется от
изменяется от 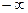 до
до 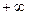 .
.
Часть годографа при 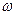 от
от 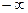 до
до 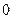 симметрична части годографа при
симметрична части годографа при 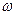 от
от 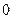 до
до 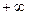 .
.
При экспериментальном определении комплексной частотной характеристики на вход системы подают гармонический сигнал 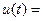 , то выход системы будет меняться по закону
, то выход системы будет меняться по закону  , причем
, причем 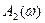 и
и 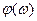 при неизменной амплитуде
при неизменной амплитуде 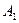 будут зависеть от частоты
будут зависеть от частоты 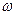 .
.
Каждому фиксированному значению частоты 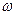 будут соответствовать определенные значения
будут соответствовать определенные значения 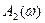 и
и 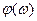 , а следовательно вычисленная для данной частоты
, а следовательно вычисленная для данной частоты
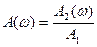 .
.
 2014-02-02
2014-02-02 3820
3820
