Пусть необходимо выявить влияние на устойчивоять САУ, например, коэффициента усиления K. Приведем характеристическое уравнение к виду D(p) = S(p) + K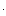 N(p), выделив члены, не зависящие от K в полином S(p), а в остальных членах, линейно зависящих от K, вынесем его за скобки. Граница D -разбиения задается уравнением
N(p), выделив члены, не зависящие от K в полином S(p), а в остальных членах, линейно зависящих от K, вынесем его за скобки. Граница D -разбиения задается уравнением
D(j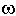 ) = S(j
) = S(j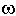 ) + K
) + K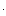 N(j
N(j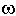 ) = 0, => K = -S(j
) = 0, => K = -S(j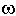 )/N(j
)/N(j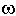 ) = X(
) = X(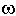 ) + jY(
) + jY( ).
).
Изменяя w от - до +
до +  , будем вычислять X(
, будем вычислять X( ) и Y(
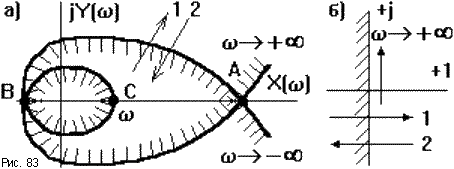
) и Y( ) и по ним строить точки границы D -разбиения. Пространство коэффициентов представляется системой координат X-Y (рис.83а). Обычно строят только половину кривой (
) и по ним строить точки границы D -разбиения. Пространство коэффициентов представляется системой координат X-Y (рис.83а). Обычно строят только половину кривой (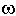 = [0, +
= [0, +  ), другую половину достраивают симметрично относительно вещественной оси.
), другую половину достраивают симметрично относительно вещественной оси.
Если в плоскости корней двигаться вдоль мнимой оси от - до +
до +  и штриховать ее слева (рис.83б), то это будет соответствовать движению вдоль линии D -разбиения при изменении w от -
и штриховать ее слева (рис.83б), то это будет соответствовать движению вдоль линии D -разбиения при изменении w от - до +
до +  и штриховке ее также слева. Переходу корня в плоскости корней из штрихованной полуплоскости в нештрихованную вдоль стрелки 1 соответствует аналогичный переход через границу D -разбиения вдоль стрелки 1, и наоборот. Если пересекается область с двойной штриховкой (точки A, В, C), то в плоскости корней мнимую ось пересекает пара комплексно сопряженных корней.
и штриховке ее также слева. Переходу корня в плоскости корней из штрихованной полуплоскости в нештрихованную вдоль стрелки 1 соответствует аналогичный переход через границу D -разбиения вдоль стрелки 1, и наоборот. Если пересекается область с двойной штриховкой (точки A, В, C), то в плоскости корней мнимую ось пересекает пара комплексно сопряженных корней.
Если известно количество правых корней, соответствующее хотя бы одной D -области, то двигаясь от нее через границы с учетом штриховок, можно обозначить все остальные области. Область с наибольшим количеством штриховок является претендентом на область устойчивости. Нужно взять любую точку из этой области и при соответствующем значении K проверить систему на устойчивость любым методом.
Есть одна особенность. Так как K - вещественное число, то Y(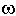 ) = 0, поэтому нас интересует не вся область устойчивости, а лишь отрезок вещественной оси в этой области, то есть K = X(
) = 0, поэтому нас интересует не вся область устойчивости, а лишь отрезок вещественной оси в этой области, то есть K = X(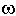 ).
).
 2014-02-02
2014-02-02 1119
1119








