Рассмотрим систему 3-х линейных уравнений с тремя неизвестными:
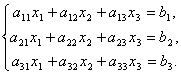
Определитель третьего порядка, соответствующий матрице системы, т.е. составленный из коэффициентов при неизвестных,

называется определителем системы.
Составим ещё три определителя следующим образом: заменим в определителе D последовательно 1, 2 и 3 столбцы столбцом свободных членов
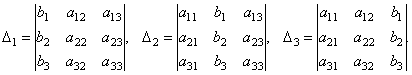
Тогда можно доказать следующий результат.
Теорема (правило Крамера). Если определитель системы Δ ≠ 0, то рассматриваемая система имеет одно и только одно решение, причём
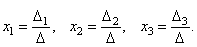
Доказательство. Итак, рассмотрим систему 3-х уравнений с тремя неизвестными. Умножим 1-ое уравнение системы на алгебраическое дополнение A11 элемента a11, 2-ое уравнение – на A21 и 3-е – на A31:

Сложим эти уравнения:
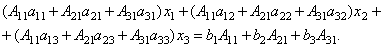
Рассмотрим каждую из скобок и правую часть этого уравнения. По теореме о разложении определителя по элементам 1-го столбца
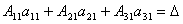 .
.
Далее рассмотрим коэффициенты при x2:
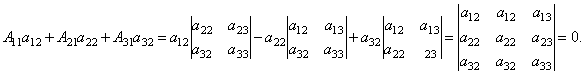
Аналогично можно показать, что и 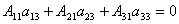 .
.
Наконец несложно заметить, что 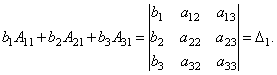
Таким образом, получаем равенство: 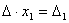 .
.
Следовательно, 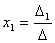 .
.
Аналогично выводятся равенства 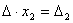 и
и 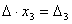 , откуда и следует утверждение теоремы.
, откуда и следует утверждение теоремы.
Таким образом, заметим, что если определитель системы Δ ≠ 0, то система имеет единственное решение и обратно. Если же определитель системы равен нулю, то система либо имеет бесконечное множество решений, либо не имеет решений, т.е. несовместна.
Примеры. Решить систему уравнений
1. 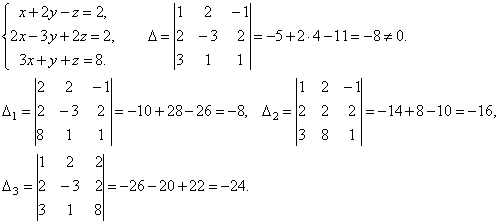
Итак, х =1, у =2, z =3.
2. Решите систему уравнений при различных значениях параметра p: 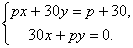
Система имеет единственное решение, если Δ ≠ 0.
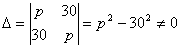 . Поэтому
. Поэтому 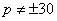 .
.
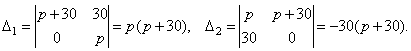
1. При 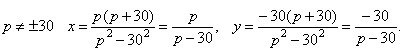
2. При p = 30 получаем систему уравнений 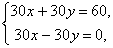 которая не имеет решений.
которая не имеет решений.
3. При p = –30 система принимает вид 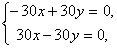 и, следовательно, имеет бесконечное множество решений x=y.
и, следовательно, имеет бесконечное множество решений x=y.
 2014-02-03
2014-02-03 8100
8100








