2014-02-02
1835
Рассмотрим таблицу из 9-ти элементов:
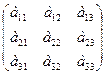(2)
Определителем 3-го порядка, соответствующий таблице (2), называется число, равное:
а11∙а22∙а33 + а21∙а23∙а31 + а21∙а32∙а13 - а13∙а22∙а31 - а11∙а32∙а23 - а21∙а12∙а33
Этот определитель обозначается символом:
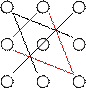
При вычислении определителя 3-го порядка удобно пользоваться правилом треугольника (правилом Саррюса):
+
|  | | |||||||
 | |||||||||
 | |||||||||
- первое действие
- второе действие
 |
Свойства определителей:
1) Равноправность строк и столбцов: определитель не изменится, если его строки заменить столбцами или наоборот
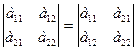
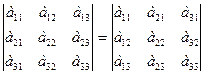
2)При перестановке двух параллельных рядов, определитель меняет знак.
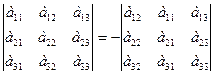
3)Определитель, имеющий два одинаковых ряда, равен 0
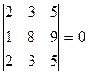
4)Общий множитель элементов какого-либо ряда определителя можно вынести за знак определителя.
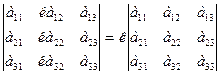
Из свойств 3 и 4 следует, что если все элементы некоторого ряда пропорциональны соответствующим элементам параллельного ряда, то такой определитель равен 0
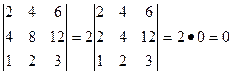
5) Если элементы какого-либо ряда определителя представляют собой суммы двух слагаемых, то определитель может быть разложен на сумму двух соответствующих определителей.
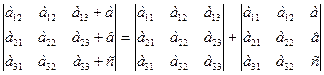
6)Элементарные преобразования определителя.
Определитель не изменится, если к элементам одного ряда прибавить соответствующие элементы параллельного ряда, умноженные на любое число.
Пример: доказать что
Доказательство:
0 (cв-ва 4 и 3)
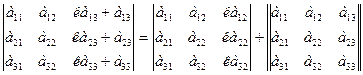
Минором некоторого элемента аij определителя n-ого порядка называется определитель n-1 –ого порядка, полученный из исходного, путем вычеркивания i – строки, j – столбца
Обозначается Мij
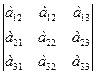
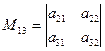
Алгебраическим дополнением элемента Аij определителя называется его минор (Мij), взятый со знаком «+», если сумма i+j – четное число, «-» если i+j – нечетное число.
А = (-1)i+j∙Mij
7)Разложение определителя по элементам некоторого ряда.
Определитель равен сумме произведений элементов некоторого ряда на соответствующие им алгебраические дополнения:
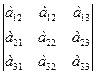= а11А11+а12А12+а13А13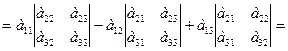
=а11(а22а33 – а23а32) – а12(а21а33 – а31а23) + а13(а21а32 – а31а22) = а11а22а33 – а11а23а32 – а12а21а33 +
+ а12а31а23 + а13а21а32 – а13а31а22
8) Сумма произведений элементов какого-либо ряда определителя на алгебраические дополнения соответствующих элементов параллельного ряда равна 0.
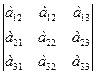= а12А11+а22А12+а23А13 = 0
Матрица.
