Нахождение ранга матрицы методом окаймляющих миноров.
Существуют другие методы нахождения ранга матрицы, которые позволяют получить результат при меньшей вычислительной работе.
Одним из таких методов является метод окаймляющих миноров.
Разберемся с понятием окаймляющего минора.
Говорят, что минор Мок (k+1)-ого порядка матрицы А окаймляет минор M порядка k матрицы А, если матрица, соответствующая минору Мок, «содержит» матрицу, соответствующую минору M.
Суть метода элементарных преобразований заключается в приведении матрицы, ранг которой нам требуется найти, к трапециевидной (в частном случае к верхней треугольной) с помощью элементарных преобразований.
Для чего это делается? Ранг матриц такого вида очень легко найти. Он равен количеству строк, содержащих хотя бы один ненулевой элемент. А так как ранг матрицы при проведении элементарных преобразований не изменяется, то полученное значение будет рангом исходной матрицы.
Рассмотрим квадратную матрицу
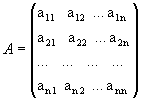 .
.
Обозначим Δ =det A.
|
|
|
Квадратная матрица В есть обратная матрица для квадратной матрицы А того же порядка, если их произведение А В = В А = Е, где Е - единичная матрица того же порядка, что и матрицы А и В.
Теорема. Для того, чтобы матрица А имела обратную матрицу, необходимо и достаточно, чтобы ее определитель был отличен от нуля.
Доказательство:
1. Необходимость. Пусть для матрицы A существует обратная матрица A-1. Покажем, что | A | ≠ 0.
Прежде всего заметим, что можно доказать следующее свойство определителей 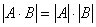 .
.
Предположим, что | A | = 0. Тогда 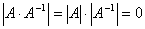 . Но с другой стороны
. Но с другой стороны 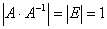 . Полученное противоречие и доказывает, что | A | ≠ 0.
. Полученное противоречие и доказывает, что | A | ≠ 0.
2. Достаточность. Для простоты доказательство проведём для случая матрицы третьего порядка. Пусть  и | A | ≠ 0.
и | A | ≠ 0.
Покажем, что в этом случае обратной матрицей будет матрица
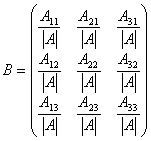 , где Aij алгебраическое дополнение элемента aij.
, где Aij алгебраическое дополнение элемента aij.
Найдём AB=C.
Заметим, что все диагональные элементы матрицы C будут равны 1. Действительно, например,
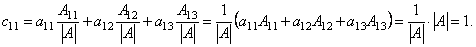
Аналогично по теореме о разложении определителя по элементам строки можно доказать, что c22 = c33 = 1.
Кроме того, все недиагональные элементы матрицы C равны нулю. Например, 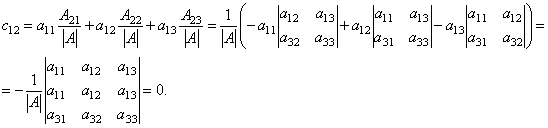
Следовательно, AB=E. Аналогично можно показать, что BA=E. Поэтому B = A-1.
Таким образом, теорема содержит способ нахождения обратной матрицы.
Если условия теоремы выполнены, то матрица обратная к матрице  находится следующим образом
находится следующим образом
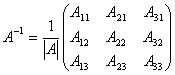 ,
,
где Aij - алгебраические дополнения элементов aij данной матрицы A.
Итак, чтобы найти обратную матрицу нужно:
1. Найти определитель матрицы A.
2. Найти алгебраические дополнения Aij всех элементов матрицы A и составить матрицу 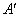 , элементами которой являются числа Aij.
, элементами которой являются числа Aij.
3. Найти матрицу, транспонированную полученной матрице 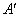 , и умножить её на
, и умножить её на 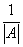 – это и будет
– это и будет 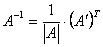 .
.
|
|
|
Аналогично для матриц второго порядка, обратной будет следующая матрица 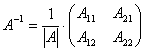 .
.
Обратная матрица матрице А, обозначается через А-1, так что В = А-1 и вычисляется по формуле
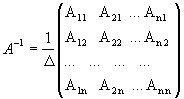 , (1)
, (1)
где А i j - алгебраические дополнения элементов a i j матрицы A..
Вычисление A-1 по формуле (1) для матриц высокого порядка очень трудоемко, поэтому на практике бывает удобно находить A-1 с помощью метода элементарных преобразований (ЭП). Любую неособенную матрицу А путем ЭП только столбцов (или только строк) можно привести к единичной матрице Е. Если совершенные над матрицей А ЭП в том же порядке применить к единичной матрице Е, то в результате получится обратная матрица. Удобно совершать ЭП над матрицами А и Е одновременно, записывая обе матрицы рядом через черту. Отметим еще раз, что при отыскании канонического вида матрицы с целью нахождения ранга матрицы можно пользоваться преобразованиями строк и столбцов. Если нужно найти обратную матрицу, в процессе преобразований следует использовать только строки или только столбцы.
Пример 1. Для матрицы 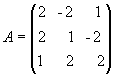 найти A-1.
найти A-1.
Решение. Находим сначала детерминант матрицы А
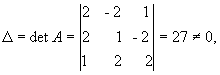 значит, обратная матрица существует и мы ее можем найти по формуле:
значит, обратная матрица существует и мы ее можем найти по формуле: 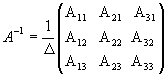 , где Аi j (i,j=1,2,3) - алгебраические дополнения элементов аi j исходной матрицы.
, где Аi j (i,j=1,2,3) - алгебраические дополнения элементов аi j исходной матрицы. 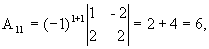
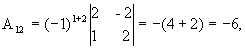
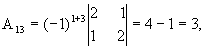
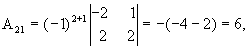
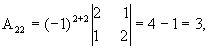
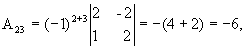
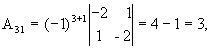
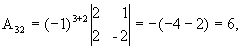
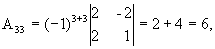
откуда 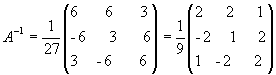 .
.
Пример 2. Методом элементарных преобразований найти A-1 для матрицы: А= 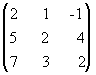 .
.
Решение. Приписываем к исходной матрице справа единичную матрицу того же порядка: 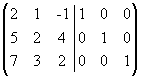 .
.
С помощью элементарных преобразований столбцов приведем левую “половину” к единичной, совершая одновременно точно такие преобразования над правой матрицей.
Для этого поменяем местами первый и второй столбцы: 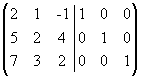
~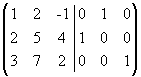 .
.
К третьему столбцу прибавим первый, а ко второму - первый, умноженный на -2: 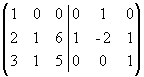 .
.
Из первого столбца вычтем удвоенный второй, а из третьего - умноженный на 6 второй; 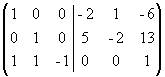 .
.
Прибавим третий столбец к первому и второму: 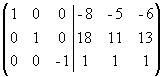 .
.
Умножим последний столбец на -1: 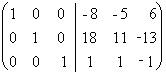 .
.
Полученная справа от вертикальной черты квадратная матрица является обратной матрицей к данной матрице А. Итак,
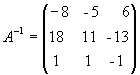 .
.
 2014-02-03
2014-02-03 5098
5098
