Математична постановка задачі. Алгоритм програми

Математична постановка задачі

1) Запишемо систему рівнянь теплопровідності, у диференціальному вигляді,  для двошарової пластини:

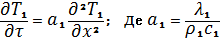  (1)

                                                                             0≤x≤X_к; 0≤τ≤τ_max ;

                                                  

 

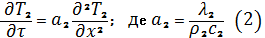
(1- для першої пластини 0≤x≤X₁, 2- для другої пластини X₁≤x≤X_к) 

2) Початкова умова:

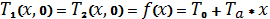
3) Граничні умови:

Оскільки поверхня стінок омивається теплоносіями, а між пластинами прийнятий ідеальний тепловий контакт, граничні умови будуть третього та четвертого роду відповідно:

1)

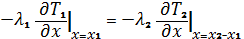
2)  

;

3)

Маємо одномірну по простору нестаціонарну задачу, для рішення якої скористаємось методом кінцевих різностей. Побудуємо сітку: по координаті візьмемо крок dx = 0,1 м. Для обчислення кроку за часом скористаємося умовою збіжності: 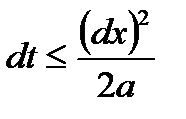і виберемо dt = 0,35 с. Будуємо сітку:

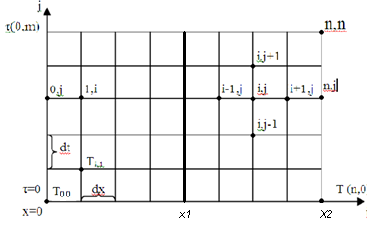
Мал.1. На малюнку зображена схема нанесення сітки на поверхню пластин.

 

Рівняння теплопровідності заміняємо кінцево-різницевим співвідношенням:

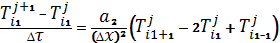
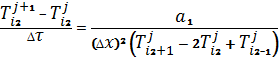
де i=1,2..N, j=1,2..M.

Початкова умова:  

Граничні умови:

1)

2)

       3)

 

Алгоритм програми

1) Ввід констант.

2) Ввід початкових даних.

3) Розрахунок температури при τ=0:

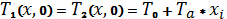
4)Розрахунок розподілу температур на границях:

А) Виконуємо розрахунок для першої пластини в заданому інтервалі x₀<x<x₁:

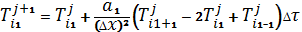
Б) Виконуємо розрахунок для другої пластини в заданому інтервалі x₁<x<x₂:

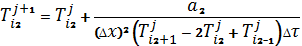
5)Виконуємо пункт 4 для інтервалу τ₀<τ<τ_кін.

6) Вивід кінцевих результатів у вигляді таблиці та графіків.

6) Кінець.

 

                                               

 

 

Блок-схема